Neural Network in Factorio (MNIST)
This is currently a work in progress...
For a more readable writeup take a look at my reddit post.
Work In Progress.........
The full end goal is MNIST(aka handwritten digit recognition), but first I'll start with a simpler example as a proof of concept, XOR.
Initially the plan is to train the neural network in Python then manually enter the weights/biases into Factorio. After I'm sure it's feasible, I will then automatically generate the weights as an ingame blueprint instead.
XOR Neural Network
This is a classic problem often used as a "Hello, World!" problem for neural networks.
XOR is a logic gate with the following truth table. If you've never encountered a truth table before, this is just showing the corresponding output given specific inputs. The tldr is: XOR outputs $1$ if and only if one of it's inputs is true, but not both.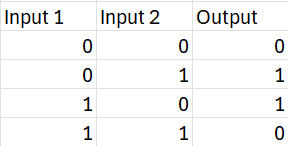
Architecture
Now onto the neural network architecture for this function. First, starting with the obvious part, we will need two inputs and a single output. Then for the hidden layer, I will choose a size of four. The resulting network is below.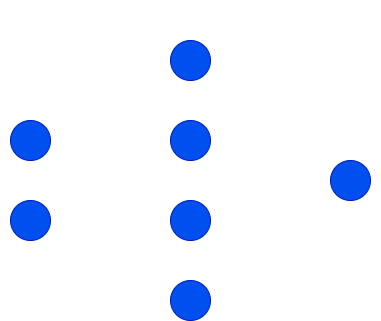
ReLU
For the hidden layer I used the ReLU activation function. ReLU is a simple function, but it serves it's purpose, introducing non-linearity into the network. Non-linearity is what enables neural networks to learn complex patterns.
$$f(x) = max(0, x)$$
It's relatively self-explanatory, but here's a graph for completeness.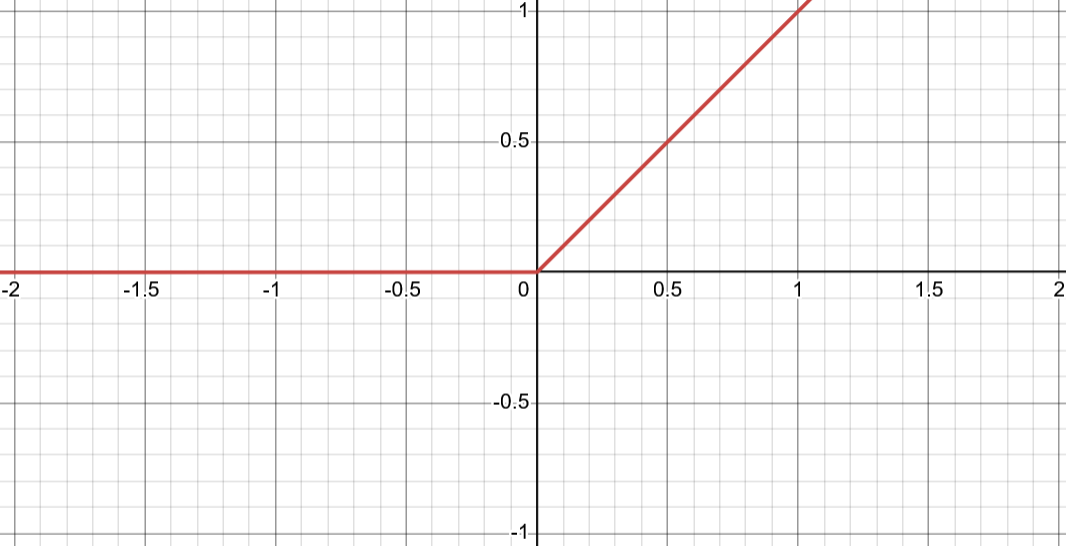
Sigmoid
For the output layer it's common to use the sigmoid activation function for binary classification problems, which XOR is. Sigmoid's output is a value between $0$ and $1$, and can be interpreted as a probability. It's often defined by the following:
$$\sigma(x) = \frac{1}{1+e^{-x}}$$
Additionally, we can actually do a simple optimization here, since we don't care about the actual output probablities just the final decision. As a result we can actually remove the sigmoid activation from the final layer during inference(however it is still needed during training for this to work).
First, here's a graph of the sigmoid function.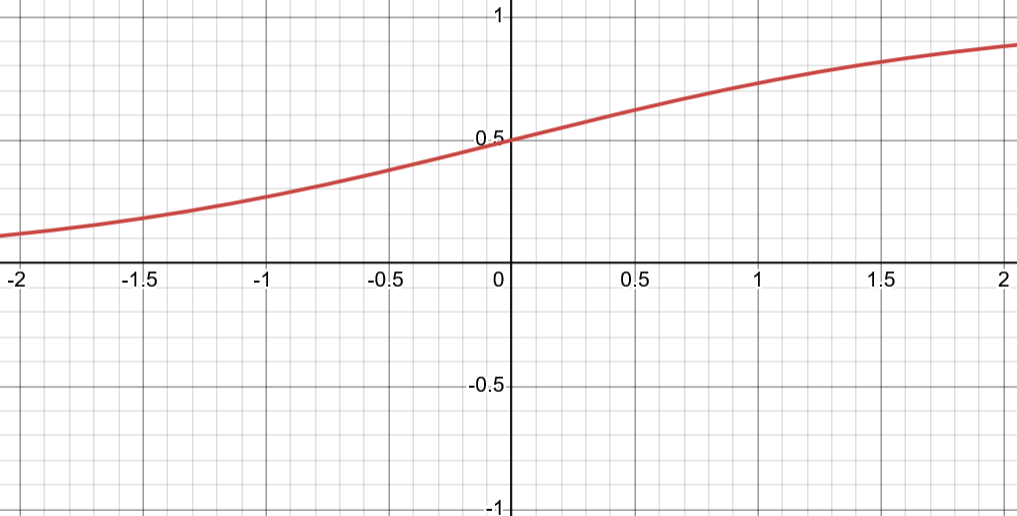
As you can see, when the input(x coordinate) is $< 0$, then the output(y coordinate) is less than $0.5$. Also, remember we are treating this output as a probablity that the XOR result is equal to $1$. So if the output is $0.5$ then that essentially means "there is a $50%$ chance the result is $1$. So looking at the graph, we can actually see that at $x = 0$ is when the transition happens. If the output falls on the left of the y-axis then the XOR result is predicted to be $0$ and if the output is on the right of the y-axis, then the XOR result is predicted to be $1$. So instead of using the sigmoid function at inference-time, we can instead just check if the would-be sigmoid input is greater or less than $0$. This may seem like an insignificant side quest, but remember, anything we need to run during inference must be implemented in Factorio, and a simple comparison operation is much easier than the sigmoid formula above.
So the formula on the left is replaced by the one on the right:
$$y = \sigma(x) = \frac{1}{1+e^{-x}} \quad \longrightarrow \quad y = x > 0$$
Quantization
Additionally, another problem that I ran into is neural networks often use floating point numbers for weights/biases, and Factorio doesn't have floating point numbers($1.4, 2.5$), only integers are supported($1, 4, 7$, etc.). As a result, I need to figure out a way to translate these large floating-point values into more-constrained integers. In this case, the transformation is called quantization, and there are many different ways to do it. For this neural network I can just multiply all the weights and biases by $1000$ and round them to the nearest integer. This is a very simple way to do the conversion, it is effectively throwing away all the other decimal places of precision and using just four of them though, so it's not ideal by any means. There are plenty of more advanced techniques1
explain XOR Factorio image/blueprint
Also, here is the Factorio blueprint string so you can import it into your own game, I will be providing blueprint strings in these boxes for the rest of the blog post. (Click the copy button in the top right!)
0eNrlm22P4jYQgP9K5Y+tudqeyRtS+xOuUj9VWq1QAN9dpBBoCNeeVvz3ztiwsGzCbXy9lhDtl2H8MjMPtscv7JOYlzu7qYuqEdMnUSzW1VZMH57EtvhY5SXrqnxlxVTkddF8WtmmWEwW69W8qPJmXYu9FEW1tH+Lqd7LllbcX5NXTXsbs3+UwlZN0RTWm3Ufvsyq3Wpua+pUXutIis16S23XFVuk/ibZu0iKLySk7yIysyxqu/Dl2kjuo6nX5WxuP+WfC+qAWm19he1LmTw5hiXFh6JsbH2pPfi1tM6zeueaTjZlXlWWXftzl5cUClWp1vWKoLD91SavnetT8YtT7Ji7AUz3j/S3Z4YXCExPBMkgEajO+EFeH4Etg8DHn1zGj+3hn7qdUfGyeGbxoai3zezVkO4Il2xtuWT5usVu87HOl/a86npjiYJzS/xIMax3zWbXvKFpKyMMZRSPh1HUm1HyfcdRS8RdcLpxnjP66ZsZxedzulja+jog7Afo0OcFnfNPD31gvVhKfhWcSnz0HQnsNYL2BScJzTnR3eScNBQBDgnBREM3giw07Q4MQaahk4FWoXkFxpNXtA6FZEYEyYRmXxhP9tUQlH7hvtKvxn4rrzouvG+dTrew7oLJ4u5lN+pHADoJ3HTqoQ2I7mYQ910wzPgW1dNOdUusy0mZrzYt64TG4wDRDk4bjkVRL3ZFM7NVPi/tUkwpUiuf1c+I+q2ox+FLs/T1gtEaUt+dp4avx/ato/0ysH/pYkNnobtsPah5TieN7sstFcpADeqwlSZRNwMdetRQwxoHVyGYwKyvBpT1JwjxlYteCESgB4QgQtMNAANzvhpPzjdRICM9Ika99474fRnd4FnTJH0ZJf8Xo9MmUiulXoL4+QqILpTtPNI37aXT/2Qn3T0Iem+oTdbzjKBu/YgAKvSIoG7zhNB9CIbQq8URJUQwgYxGlBABAm9f1XgSImDI5au6r7tXiMKOIIM6hBnQWfeSG3jvOKYVN/SBHIZ0XaHjpPukCqEP5OZubq0g9IEchvU+fm0YYOj7OI7op2mhe9hoRIxCX8dxPPszDHocx/vanyEG5p14oKmXwP1FTrOxBy21BKkf5YMhKXISSJJTaZyIpGQJqThxxUjFoA7KY3FEUuykmCTtxZTaaOUaZSwaJ5LmuX+SkfVOZl905uvokxGST3UMy+Blds5485rdI6uuLUUhzUFmb4z3RidcJ/X6lPvXXs8yeltGMQ/tgTg2BzhMx6CXgWWPyjgYhMHLz7ZMdCbHXCf2dZw/idcnLHsOhvmAR8VhS/DxOhm9n8AcwMcO7A/4WMCc6ZkJ+eNk5gCeA7APNNvZB2AOeLDFdtF/L8jfBXq7yLGjjxf1mZ5tIduiQVQ0dkWD7PS/DlKU+dzSHBR//Pb7D+/fk+IzDWo3N6LYZJhlURTpFGPc7/8BPvrOXg==
Factorio XOR Implementation
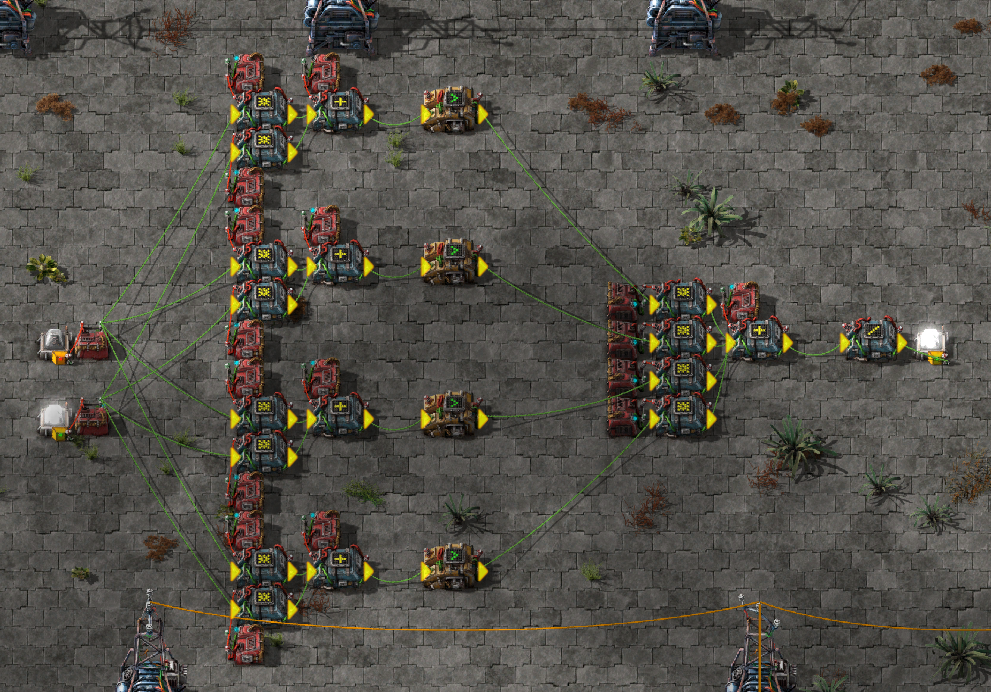
explain... label important parts...
MNIST Neural Network
next, I'm ready to tackle the full problem...
first try some simple nns on MNIST and report accuracy:
784 -> 128 -> 10:
784 -> 64 -> 10:
Binarize
however, the pixel input is grayscale, lamps in factorio are either on or off(1/0)
so need to binarize inputs
mention loss in accuracy, for ex. 96.84% -> 96.51%
Reduce Input Size
also, 784 is a lot if inputs, will need to do a 1x784 * 784x128 matrix multiplication not easy in Factorio...
Downscaling
try downscaling to a few different resolutions,
28x28: 96.51%
24x24: 95.72%
20x20: 95.62%
16x16: 94.17%
12x12: 89.78%
8x8: 70.61%
going to 12x12 causes some continuity issues,
for example data item 0 of the training set, the 5 gets disconnected
can show the same image in 8x8 just for fun...
tldr will go with 16x16
Removing Borders
can go a step further and remove a 1-pixel border on the 16x16 images as well.
This is fine because most of the time the edges of the image don't have useful stuff anyway.
Also, this will bring the input image size from 16x16 to 14x14, which is a reduction from 256 to 196 for the input layer size.
14x14: 94.12%Also, try it with 12x12, so removing a 2 pixel border.
12x12: 94.22%
10x10: 93.66%
8x8: 91.22%
Removing Corner Pixels
I also had another idea! I can try to get rid of the corner pixels, even removing 4 pixels would be a win in my book.
Digits should almost always not occupy these pixels anyway.
However, unfortuantely, because I already cropped the images so much, now the digits are often pressed against the edges.
Other Approaches
(If I was reading, I would think why not use conv layers?, explain they are too complicated for factorio inference)
New technique inspired partially by Local Binary Patterns (LBP).
slide a 3x3 window over the image with a stride of 3, and convert each one to a single number/feature.
a sum over the window will not preserve position information, instead what if each pixel corresponds to a binary position
the max value will be 9 1's in binary since the image has been binarized, which represents the number 511,
and the max value a signal can be is 2,147,483,647(2^31-1), so I have plenty of leeway.
for some reason the second approach did not work well... use sum instead
2x2 window(sum): 91.14%
2x2 window:
used 0 for padding
3x3 window:
4x4 window:
Binarize Thresholds
accuracy for each threshold...
0.2:
0.5:
0.8:
Hidden Layer Size
also have to play with the hidden layer size
64:
32:
16:
8: (LOSSY) 84.71%
4:
Adding a Second Hidden Layer
adding a second layer, making the network deeper
same size as bottleneck layer for in/out
Matrix Multiplication Issue
now, the real challenge, actually implementing it in factorio
matrix multiplication issue, it's not very efficient
go back to the XOR example, for each neuron on the left, a multiply must be added for each nueron on the right
MAC Array
talk about MAC arrays, Multiply-accumulate array
show visualization/image as well
maybe even in factorio?
will need a concept of cycles/clock for this though?? didn't need it before
show 2x2 when going over MAC arrays, it's simple and can be used to explain
2x2 matmul in factorio
insert image, and provide a collapsible copy widget for the string
(insert image and bp string here)
can talk about splitting a 10x10 matmul into 4 5x5 matmuls
this makes it easier since I'll just have to make 5x5 modules and can copy and paste
go through a 2x2 * 2x2 example
might need to also pick a bigger example as well because it will just be combining single numbers
(so basically 4x4 * 4x4)
tldr since I have a couple 10x10 layers, just need to get to 5x5 then copy and paste
Factorio Implementation Progression
Single Cycle
2x2 matmul
0eNrtnNtu2zAMht9Fl4M6RPJRAfYkRRA4qdYa8CGz5XZB4XcfKblNsiVrLM8ogvGOYWnxJx37E2Gnr2xTdHrX5JVhy1eWb+uqZcv7V9bmj1VWoK/KSs2WLGty81Rqk2/vtnW5yavM1A3rOcurB/2TLUW/4kxXJje5dkvYD/t11ZUb3UAAf1vqIW93Rba/22WVLhhnu7qFo+oKs8FKd1Itvkac7dkySr5GkAJUmaYu1hv9lD3nkBYCd1kDqxnduGQQ8vC+yPe8ac36UILZ7zDvc96YLsOMgxAXcaefdbM3T3n1yFyy1mTYjwV+KDERlrpk32y5W5fjgzUXrO/5PLLEBFliPllygiw5n6xggqxgPlnhBFnhfLKiCbKi+WTFE2TF88lKJshK5pOVTpCVzidLTZClQNYKwrPiJdu36/apfmFL03Qaxf4GGnk9aFJFoCHQEGgINAQaAs1Y0ASHg7sN5LZlnKOMHBjTn1kkfF/krYDj+eqvw5G6yKxWb/GY9tQGer0Naxx6Xbwz7eD9oDs4LILzB/wNagB/VTeljfut4ejo7HUO3Vz15wqPfObBlDBNmCZME6YJ04TpKzEdjyXsYSq8BcLGFwmb+AzCRFgiLBGWCEuEJcJeS9jUe4aNFzdA2OQiYZX31uImCk8vFi4WI6b3+K1mSXsL2lvQ3oL2FrS3oL3FlXsLIXxIExBpiDREGiINkYZIcy1pRrw4pCKaaYg0RBoiDZGGSDOaNIEPaWimIdIQaYg0RBoizdWkGf96afgxb+Z6QvXYaF2Ne0QVXH5EFfmXLm+hdHG59NGvPKngpkqXl0tP/Eu/iS98eLn0w2P48z/WPfsg/rj0h7xxxQ1M/rMRh4XX77fF1uO+6AqHlNBNWOf6A+1DbDiu3unGvXC/ZF8gqu7MrhshYK+LAu6b/flOKv9OSurk8W/xFuM7mabUyTOdFP6dpKv7pJPSo5PBP+rk0JGTwfq02vOaAw/N4pM1h/530Yi+scedjPyvferkSSdj/2s//KzrKPG/9j9N84S9aEzf2ONOKv9r/3/u5IqzFygcB7J7wSUPuVzxewlWbK2QCw77fAFmBM7UOmNwwpYVnQk4lXWm6AytU6EZWVMscIHBFmi7ECHRjp0doJ04GwRw4dIIzCjc6hAqcXlrY1I5xKQHgXgYhw3g4A+4HNZX6F84v0K/tH4sAeMHG/yBswXaTg+GYt4A7cDVZW1sDGgQzpbot52L0O/0yNjF2PjE+a1tdWJd0P3c6BLOzOH/S3FWZBsNp5HJn7LMTNnhCXyGodme8CiWKlQqSoIoCBPZ978AySVuoA==
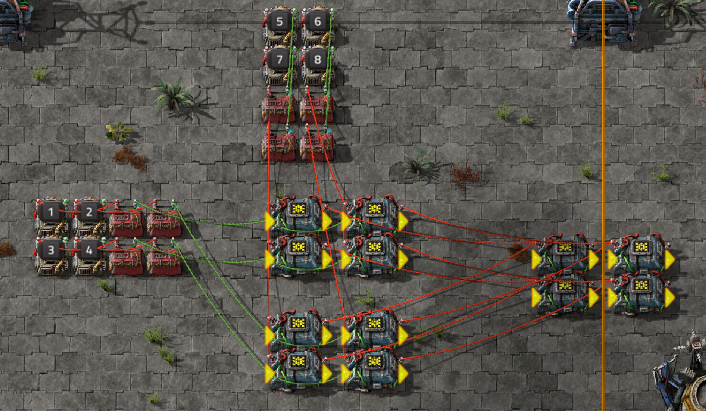
3x3 matmul
0eNrtnetu2zgQhV9loZ8LtZB4V4B9kiIInFTbCPBtZTltUPjdl0P6ptZqpXENg8D51VOHImcOaX0jmZa/Z8/zbb1um2WXPXzPmpfVcpM9fPqebZovy9mcXlvOFnX2kM3apntd1F3z8uFltXhulrNu1Wa7PGuWn+tv2UO5yy8cRf11s2V3+Rixe8yzetk1XVPHYcN/3p+W28Vz3fpO80NHn5vNej57/7CeLet5lmfr1cYftVrSWL6nD+qjzrN336X8qP0AftyuXc2fnuvX2VvjB/XN1rPW99XVbRzKN/l87OLfpt10T6fwu/c1jfrWtN12RuPtw4gtPtRvdfvevTbLL1kcLCSZPRT0nwUNRIk+ZP+EZF/iGL/ps8h2ZOEtwiqvCKu8XVjiirDE7cKSV4QlbxeWuiIsdbuw9BVh6duFZa4Iy9wuLHtFWPZ2YbkrwnK3C6u6IqzKh/Xom8/mX2fvm6fN6+pr9tC125qC/QEzYjRmJDADzAAzwAwwA8xMxYwcjRkBzAAzwAwwA8wAM1Mxo0ZjpiwPnNHgDDgDzoAz4Aw4M5IzejxnCnAGnAFnwBlwBpyZyhkzmjMVMAPMADPADDADzEzFjM1/tWntZ9i438NmU7/QEZu+9tg57JnLvUnzI4xOr/4mrS9tXS/9q//5P/oU/B+Wq3YRGv5gFb2wDWd/78Pjbnchbzcxb5tU3mIw72pi3iapvOVg3mUxfVMl6inUU6inUE+hnkI9NbaeKhmb9xU4A86AM+AMOAPOjOUMY/c+rmfAGXAGnAFnwJnRnGFs3wdnwBlwBpwBZ8CZ0ZxR0zmD+2bgDDgDzoAz4Mxozujp983AGXAGnAFnwBlwZjRnTvv3N9tnP3jI48KXxFRkjLm4ac0yvtRsQSvQCrQCrUAr0GosrRwDNAagAWgAGoAGoAFoxoKmYjw+A1c0AA1AA9AANADN6IebFwzQ4IoGoAFoABqABqAZDZpy+oOacEEDzoAz4Aw4A86M5oyYzhlcz4Az4Aw4A86AM6M5I7lPBLQpPCHODj4hTihu4iaFxNVw4pr7LMQkZtwNJ264iScx43o4cct9CmQSM14NJ+64iScx42Y48anP/VT3m3H6bfY/9RaXBTdvk0DewwtdlhPzlinN9/CZTYqJeYuU8h5+rK+U3PlOYZ0Pn9ek4s53CnkPP85Y6lFfL/nVl0uk4Z4aXQLWDdf50nLfKinkPVzmS8d9q6SQ9/CT3mXFnG9ZJl0CqII530nkPYwENbX0KVPKexgJamrpow95y7TvXyjJTVyk/RsW6lT8zNqme13UXfPyG4afz/jnpo2p7W+o/2zDqdun4z3NDeOmZkzbD+m99P2MPzC8Qfxxq3XdxhrnIfvbt1ptu/V2QgDv9Xy++prtLvuouT4K+Hjuo5nso8B6vOCj5fqI9djz0U31scByvGBjxbQRq7H3w8EFt0xRaX+wprn3IqVO+t6z5t6LTCLv4XuwWnLLKYUTxrmPinshq5O+l601t/zB+un5aJjcho09Gy2X2zbtXQLacRM3af9Gpq64ALN455z/hHnB9dHAx3MfSy4QsR57Pgquj1iPPR8ls7DAcuzZqJg2YjX2bJx8uaD/0Grc29H7yks/1csBT67L7Z0Dnnw/urpzwOzK1aW9o9mw9zpUSe/psey9DlXSe3psya2wHRhy7qPg3mqrkt4bZSW3Isb66fnILeVgY89GbilX3anQsIYZsLtXwJZZe97NYccM+G4OV8xi+V4Ou4IZ8L0cdiWzuldl2l/ictwdnqpIIfHhra2O+4nyfsbB172P3A2j+wUEH/c+cj+hxnrs+8jdMIr12PfR8i4/sBz7NjL3i2I19m2suGWKSPvpAhX3826FnbI9H7mfd8PHvo+CeT6DjT0b5aSf8lPqYidqwhe2qYvHPPvqJ4DOZ5/KXOSyyMVj/kmQlEFKkipIlZe5zUuvtFcuKONVFVRZUEsTWpbUl6iiDp3ZqENvLmpFWkStSZdRm1znUuf6oL0zQfuhcyHjWI60iroirYMWBWkTdUk6xisE6RgxdZ17o6hPSceqeKyiY1Vsr+hYFfNSFL/aO0Dx+/ZBq7NjSWt50L6NObSRuY3x0GHUv4ha5mZ/rDkbl7Q+vu7bR6+89v3E+KkLik1E7fvZ9+/OYiatj6/L3BVRV9R+P4c0XzpOsqZ8TWyjySsjoqZ8dczXax9DjE1Tvib6T3+msUTUvs2+/xBzjEdTzDrGrH1KNFbQ1dm4pG150L5NeWhz9JAOo9hE1EcPTXmKOWgrD9q3jzl6ffSQuqD4RdRHD33TY15B26M+emjUyUMT3gj+BdI0d/5aI2haq77QC5rytTEXU8X2dKwtYvugKU4b47TlyWcrYj9B01zYGLOVJ5+tOvlMh+W+QKBxbYhHRk3xeOAFTWvDX1sGTfH4EzhpF+KxUVM8LsbjyCsXx3XyFH/QVXHQgvoMbWj9u7genD7lGHRVHrSgsUIbWucurnNnT/kGXcU5dbQeqrhm6B/qJ2iKs4rrgU4T8X3tT2pNVy/8SZDO3Ou28QVVns1nz7U/S2fym/xrMesWWzpBv/laLpwXtRGVqiptpZbKit3uf8z7VkU=
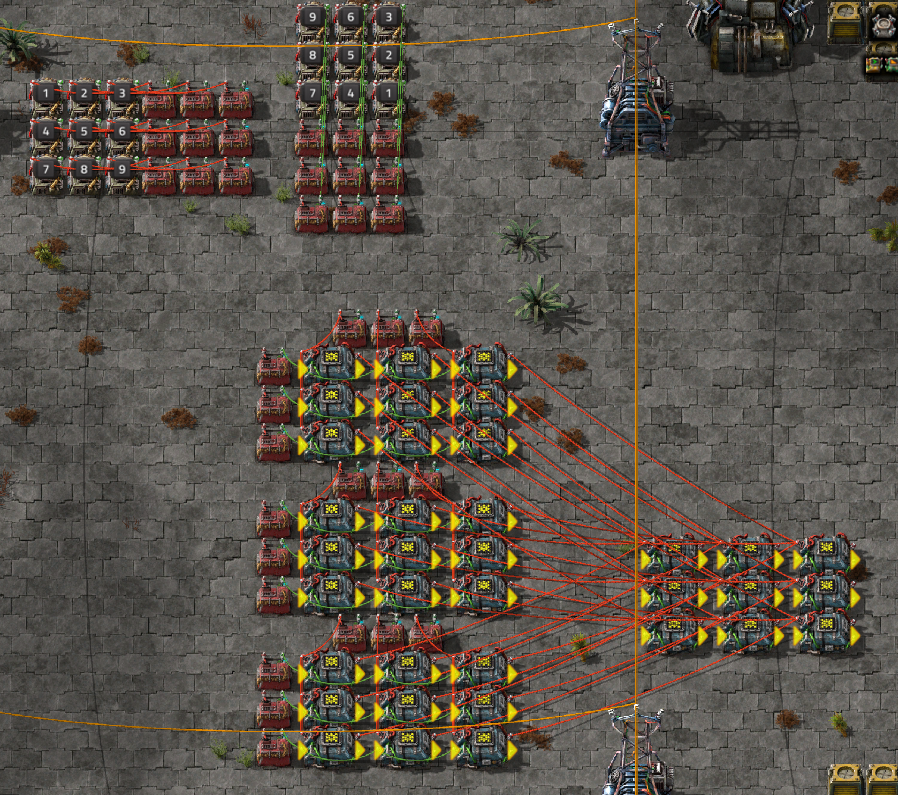
4x4 matmul
0eNrtXe1u2zoSfZWFfi7UC/FbCrBPUhSFk3pbA4mTdZz2BkXefTlD2pZcOxUnNzB47/ljDCVSmjk85iFFivrZXN8+LR82q/W2ufrZrG7u14/N1cefzePq63pxS8fWi7tlc9UsNqvtt7vldnXz4eb+7nq1XmzvN81L26zWX5Z/NlfqpT1Riq63Xay3p8vol09ts1xvV9vVMt2WE8+f109318tNvGi7u9CX1ePD7eL5w8Nivbxt2ubh/jGWul/TveKVPnR/uLZ5bq5s+MPFG8T7bjf3t5+vl98W31fxpjHbw2ITr7VdbtKtYpYv+0v8d7V53H4+uL99fqC7fl9ttk8Lul92I+X4sPy+3Dxvv63WX5t0Mw6yueoocUc3okCvmv9wsDfpHr+5Zte8EITv4ZZ6g1vq/dzSb3BLv59b5g1umfdzy77BLft+brk3uOXezy3/Brf8+7kV3uBWeD+3+je41b+fW8Mb3BqiW59i9sXtj8Xz4+fHb/c/mqvt5mlJzh7JjJ4tM2onMx4yA5mBzEBmIDOQmZkyY8plBqMZyAxkBjIDmYHMzJUZW/7QDKMZyAxkBjIDmYHMzJUZN1dmMDUDlYHKQGWgMlCZYpXxc1UGMzNQGagMVAYqA5UpVplQrDIYy0BloDJQGagMVGauyvTFT8wwloHKQGWgMlAZqMxclRnmrzLb68wAnYHOQGegM9AZ6MxMnVGdQGh6CA2EBkIDoYHQQGjmCs38XQAGDGigM9AZ6Ax0BjpTrDO6XGcwnoHOQGegM9AZ6MxsnZm/D0CP8Qx0BjoDnYHOQGeKdcaW6wzGM9AZ6Ax0BjoDnZmtM4edAE5t9/yr2vjfq83j8oZKPE7tqDu73abbiNLtXo0OR38T19fNcrmOR/8XT8YY4on1/eaOMx5hRQeeuPmPQHx6eTkVuJcGPtQQuD4f+Oz3pT4EjGDRs0DPAj0L9CzQsyjuWfTlOoMRLHQGOgOdgc5AZ2brzFA4kHNVDeTM2YGc7goDt1UFbs8HrqQ13tc9dNdaWuN95VQ3hYGbqqjuzgdupYH3lf/HXflG2HhKhdEDRg8YPWD0gNHD7K/H+XKdwVMq6Ax0BjoDnYHOzNaZUP79OOgMdAY6A52BzkBnZutMX64zeG4GnYHOQGegM9CZ2TozFH91AcMZyAxkBjIDmYHMzJUZ0xXLDEYzkBnIDGQGMgOZmS0zqvjrPpAZyAxkBjIDmYHMzJYZXSwzeGgGmYHMQGYgM5CZ2TJzeFvq8ek63pzjOLEAwLLGuO7UCzjGln8hyCmoFdQKagW1glpBreaqlRMITQehgdBAaCA0EBoIzVyh8cWfCMKABjoDnYHOQGegM/N1JhR/ugE6A52BzkBnoDPQmfk605ePZ/DcDDoDnYHOQGegM7N1Zigfz0BnoDPQGegMdAY6M1dnbCf8ItsrT8+q2OvaKmngXd3bultd/IkgPClFzwI9C/Qs0LNAz2J+z8KU6wxGsNAZ6Ax0BjoDnZmtM1b4YbI6RrDnP1NlnfDDZHUE7s8H7qU13lX+zCJIa7yrnOq98ItsdVA9nA98kAbe1f0fd6XPJdXlavz69mn5VzHdlT6W7GqK+3zT5rS0vru64zbS+q4h7vNPoV1hr62qv/f5j8m6wj5bVbX9StheWNs1hK3Ohx2Eta3q/m/3s7bCeG0jDDdIm0Vdtfz7Thq3qSDu8909r6TyX0Pc5/v3Xtzt0XXXtxG2jLrq3p6X9npM3WE7Ydi6ah30XkhyU7eGlT6l2r8o4epmeelDqr6muF+heWlfLdQU9/lBTRAvnXNVj2qCEjZrrupmLWihiNXdqoXCnpr+ezRqobCnZv4mbVrpnKLa13eoYcLhlci9OHJfQ+SvtOeH/tpis9p+u1tuVze/iV2N6/zLapNiy+tcfsXhcN3P+6UGj4K1BinueMsIZrzO/IL8H4nl7h+Wm/Q46qr5d8x1/7R9eCpw4Hl5e3v/o3k5DWQvBtIDyDGQQzGQAwj5K459J8URfJzgqIpxDODjCRy1FEfwcYKjKcbRgY8ncLRSHMHHCY6lo4a6Bg3nR4m9lwbu6x4t9YIxA1qgEzj2UhzRAk1wLB4xgI4nYBw6IYxg4wTG4vGCARtPwKiFMIKNExiLRwsYLJyC0QphBBsnMMpnGIa6394Z5DMMfd3DpEE+wzDgzzMGUj7D0APIMZDiGQYQcoyj6sRTDCDkFEjxHAMYOQVSPMkARk6BFM8ygJFTIMXTDGDkFEjxPMNQ9/vvqhNPNPR1D5pUJ55pQCs0BVI81YBWaAqkdK4BhJzgqKSTDeDjFEfpbAP4OMVROt0APk5xlM43gI9THKUTDuDjFEdXimP/F/Ex4zHZYnQa6xmPfbEydpd2ubibTs3tZV0u7hAre2mXB+GrtV5VvV2A0p3w3Vpf93ZgSivhy7W+7v3AlNbCt2t93ZvnKG1k75lW/xe3steKq4g7vBK3k71gW33L5mVv2FbfsAVZdzTHfYFeh+6FHncX83gQdqAvB7LppC5fDGWjhH3+C6KspS5fDmUjHKZcEGUrdflyKIuXJXpT+QybEa9L9LrudYnKiBcm5lrHQ7YdkuKViZlEQHKHpHRpIig5BdJKlyaCkUdASpcmgpFHQEqXJoKRR0BKlyaCkUdASpcmgpFHQEqXJtYxfHjlOZ6VLk2sY/TwysDJSpcmohU6AlK6NBGt0BGQwqWJIOQURydcmgg+HuEoXJoIPh7hKFyaCD4e4Shcmgg+HuEoXJoIPh7hKFya+HYcpfMkTro08YIuS5cmXtBl6dLEC7o8iGeRXN2fKlXFH+06hG4rH/x7JZ72cZCCCZJajKQFkhMkjXTeB5ScAmmlQIKRUyCddN4HjJwC6aVAgpFTIIN03geMnALZS4EEI6dADtJppCqGD6+8AFD8Hbm6Rg+vDJyCks77oBWaAqmlQKIVmgJphBM/IOQURyvEEXyc4uiEEz/g4xRHL8QRfJziGIQTP+DjFMdeiOM/mY+f2uZHDJy6rB9Vq1sXfz61HzWZmk1DZsemJdOw6cgMbHoyPZuBTMtmT6Zjc2hVq3yroqk6sl2yFdlDsnW0tUq2IbtLtiVbJzuQbZLdk23Z1uSLTx5qdmZINnnjUxCa3PE5toHs5JrpyE4eG4rfp0AMAeBTqMa0rnV968gmf2zyzTiyk8/Gk538MeSnTTEa8tOm2A3hYAPbluK1fbIpXptw8FQ2pOOeyvbpXp7K9gmHQBj26V6BMOxT/kDXHFL+QNcccn7yecj5CauQ6i0QVvFebI/uy/awt2OeYZfHtH38IZvw7BPm0TbkAx8fDj6zTZsZ50QskCog2rHAwAXoGhSYTrahAPi4OgTMNu1BmxOxQKqZaMcCKhWgGusz9zQd1+m4OaDFNm0dmhMxk0mZLNk22QRRnyDqCaI+QdSHA9Rs0+5/OaEpnJwp3kPnEwTSkEAifFqVmd8Ph5pim/ZtywlNAelkxxImnaCrUEQ62XSpRKpBHSqabdpyKyc0haeTTZfKJwioIQFFGLW0zwyfMAeesE27JeUEFc8Jy0VShANhNSSsBsJqSFgNIwrR6XYYdsdj4S5xiPIyP3RKGEaUz4yZQ0Vb2spZpwRlS9zhskwMnVOGkUznxqTh4i3tvqtzinKqnFPzOZvPJUh0PjdmDKXonMnnEhI2pxxfJeSreE71OTWmC+fhGHbn4lVcbhI7xkR1+RyDokM+N2YKl+cYdE7RVXIjqxgXlXFRjIvODa0ak4TLc0Q6p+gq+X6KcVEZF8W4mNxEqzE/GJGWJthTinExuaEmyre0GpVRIta2tBQwpRgXl7HmNp2WwaQUR2vyNTXrRm54aQMXSuUYSB5alRtf2uoj3SGlbL57Srl8v5Ty+X4pxb6E7ItmX2zIKfYlZM9M8iVz0LAvsS1NKfbFZWYZ9iXk2Fk7aLlUSjFfTOaLYb6YzBdWkH3sKeX1PkU5h31Oc/DTMHtsZo9h9uyQZ/XZI5hS3u5TVC5zyTCXdvFZ5pLNXLLMpV392Uk9pJT3+xSVy8yyiVkZF8vMsplZlpm1YwGr4b42U8r3+5Q5IGiZZzu+WMbTZjwt42kznjaMWWB3Nb1LaY425WQEc3eHjo64ZHcs2KU0R8Q5HaOUe0x0dMQzt2PILqU5hpSTkchdJjo6YqTbsSelmLshI+iYuyEj4VJELqeYuyFzwrGfuetDyyo0cyml1JhZnj3LnR5KmcP9PPuZO0qUMof/ijdjLlH5VuXuFaXMwU8qzwzROWUO/yrvxuzxXJs+12ZMmUN8nuvW57qNKXP4//kw5ovnf8cOCc//h92/0TMuIeMSGJeQcQlqzJDAuISMS2AkQkYimDEnAscecuyBow052uDGLOB+mModMc7DnqVU2Nd77J2vtsu72HOnrv/DZrXexs787eJ6Gbv5jf3T/utusb17oh7+9+XmkUcEzuvBDoMLxhkb9MvL/wF8GeGU
8x8 matmul, using 4x4 modules
blocked matrix multiplication
C11 = A11B11+A12B21
C12 = A11B12+A12B22
C21 = A21B11+A22B21
C22 = A21B12+A22B22
C = C11 C12
C21 C22

Multi Cycle
wait... I think i can do a mux-type thing
each row/col can be a different item
since the selector can only sort by quantity in descending/ascending
I can have a separate thing that sorts all the row/col items correctly
so like, row/col 1 can be green, row/col 2 can be blue
then I have signals going into the selector that are 1 green and 2 blue
this will cause them to be sorted (green, blue), then I can iterate by setting the selector value
(it will output 1 of the selected signal)
then all the signals go into combinators for each input and I multiply by the item from the selector
this will cause only the current row/col weights to be selected
then I shove that into the MAC array inputs
3x3 multi-cycle matmul
0eNrtXWty2zgSvsoUf+1uMVPEiyBcNXOI/ZtKqWiZiVmj11K0HW9KB9h77Mn2JItGk5LskDEBRXIo9h+r8WCju9HA13iQ/hbdLh6KTVWu6ujmW1TO16ttdPPxW7Qtv6zyBeSt8mUR3UR5Vdb3y6Iu5x/m6+VtucrrdRXt4qhc3RVfoxu2izueAn51vqq7n+G7T3FUrOqyLgts1iWeZ6uH5W1RWaZxy+iu3G4W+fOHTb4qFlEcbdZb+9R6BW1ZTin7XcXRs31C/a5sA7bdulovZrfFff5Y2kZttU1eWV51UWFTtsrdnsXnstrWs4P49fMGWn0sq/ohh/YaMbDGh+KxqJ7r+3L1JcLGnJLRTQKJJTQEit5Efzhl59jGGzyTaAcmPIdY7ASx2PnE4ieIxc8nljhBLHE+seQJYsnziaVOEEudT6z0BLHS84mlTxBLn0+s7ASxsvOJZU4Qy1ixPtnq+eIpf97Otvfrp+imrh4KEPYVzPDBMJMQzBDMEMwQzBDMEMz4wowYDDOcYIZghmCGYIZghmDGF2bkUJhRooUZTTBDMEMwQzBDMEMwMxBm1GCYUQQzBDMEMwQzBDMEM74wkw6GGUkwQzBDMEMwQzBDMOMLMzr+0ZW178FGvw0222IOT2xf0hZ22htzsTXSYg9Gh9w31PpSFcXK5v7LFloVbMFqXS1dxVemgowHN81aO3za7Tr0zjz1TkelN+vV23jqnY1Kb9GrN0v8r1SmFE9RPEXxFMVTFE9RPDUwnmLM/04l4QzhDOEM4QzhDOHMYJzh/usZ2h8mnCGcIZwhnCGcGYwzwn89QzhDOEM4QzhDOEM4MxhnpP9LYrRvRjhDOEM4QzhDODMYZ5Q/ztB6hnCGcIZwhnCGcGYwzqT+byNnhDOEM4QzhDOEM4QzQ3FG++OMIZwhnCGcIZwhnCGcGYozmf9nL2g9QzhDOEM4QzhDODMYZ4w/ztB6hnCGcIZwhnCGcGbwv75I/L+vROsZwhnCGcIZwhnCmcE4w/xxhtYzhDOEM4QzhDOEM4Nxhod+0C4bw4fdZO+H3bgI/YKhGYPiWb/iMrTHR6G47ldchfb4KFxd9Suehn68cRSKp/2K61DFR+Hqpl9xz8+UHt7Bv7zi8A/Vf9rc5vmZ0sM3brIR6N3v6CIJ7e8x6N3v54KF9vcY/Lx/RheeUdvhnbQx9Hf/13iFCNV7DP3d/9VpIQOBjDOn911ZoWbNeudyVvhnyAeo7UpnOwNhP+eLbdFpEBU44fFkBI7QH8OKNHDCG4Xe/as1oQMH/ij07v/sujgEctuHW6u30/E7daVBZXknj0NQVFf5artZV/WH22JRd8wbe3cRr+cN2fWfM5PhnEUv56yLMxvOmffL3N3x87KaP5T1rCryu9l9vrqbQS0rwRa3SeJ9jTYfqy7Xd1agpMvG8uizisW8vCuqN5aWfhI3PGf7nSbntMepj/47T/n8Hvecjpzyz2j3KY7WD/XmoUaunvx6/Fj67raYtlP5uFdiUoYqLka9EpMqFKj4uP9hhAxGaDHqEFXq0IiMj3uTSYbutYyiw/vXoNIMCk1S/YPQRHnuW8j97KgGIue5LFmuPq9/VpCnWECAJq0Bunh5BiLMz5xBgUhruXq9Kt4+nfcOZFxX/PB0/X//+W8Uv2A7WxX107r6y4lfFXdt4IczQ7PubLkUs0YCGyqGx0etmN+17BrbN+3O6focRQTE2/J11zLexVoGBNwdrC8WcSvl5+jiAo7+5l7I7nt/P82d+hzF98RHvZxXf+2ZNOmfSX0PfOT76R3079nifQP8LNHdgb94k/9zsVisn35W3KyyoBW0nMoKWpnQhaS8uGuHeEb/nmeahK6oxqF5f2CYstClxTg079/vTQ9h7LZYWDHXb0wHjd7pwOlgvSkqXLC0DVieSMyW+dd9UObU9w1FOxUSQdNbenXTG/DbPM+cB8w+V+vlrFxZXm3M3eMOh+g0r8r6flnU5Xzg9JcOOv86sH1lw0Cj2aFl2fg/d+yY/4haSw/hc59vig/366r8t1XPluyCVjwv5J4NWqt0dpjy7bDDrE0d9h4dlnp3WEId9p4dpr0AJW36Sv8qGz0Btnu3vaGOPvm5e0NN8HTa7lCaeQ9hz6jpTEP4hZuED88Xi6hOAxm/IaMvMGQuuWXUelmP/+jE23/0pPxHM18DgUmnZCC/w4fWOoRJV4tJWngPGT6tISP9hgyfGCZ5ryP1tGIanfr5Dy0Drn7K1d5DZmJhnN9Jk57aMsD3oGm/cWfG/UZwloQqno3j8LhXcc9jpsPdkmwUx0z9h86Z79vv/P00/5mXNTMR2uNmFD3ef1szk6E9Pu43BjPvQFq98PR3iwouvb//WFRWhffe3c/S0O4y1F3v0F3a/3z60qPrO3MN77GOg69T4/N9ENppzizUnIbM2WFO438YT97Za06ThJqTvLPLnN6nKqkg7+w3Jw81J3lnlzlF6KG6mcZumpGhp8ZTMZAKPTWeioE8X1bRrzZhru7jJkaHHppOxWOy0FPBqRjIhJ4BTcRALAnd7BfJuL+CyZLQ3f530Dxk79f8QPXQ7X6RjPpjHCwRgduJjeK0nXjR7USWyMANsAv214gWcSxRgVs2ZM9ue6aBmwxkz257Br3MMdiYdItrdLe4WJKFvKxwXpf4hW4pscSE3DWnIXPFQ4YlgRtJ4kq/kssYC7ldPp1JhPGQ29M0iVzzJCJCbgdPaMjIwAMxwSeytchUUDAvaFK53kklDTwknc6g0UHLHTGZaTcLPEWejgeFLQhp2r3eaZcngQfpkxk0PGyBOJlpl/PAmwbT8SARtISmafeKp10ZePtkOoNGBW0yTGfaDb0SKOQ17ORasz5ZDaDpjyzmMTcx/xR/tEQsEkcKILkjZcziLGaWUpYyjkotpR3FEqjJXE3meGVIO2Yp0o6bQloCLZBWQGukgaVFQ8dTAy2RzoBOkTZAY7s29LK0QpoBLRwtQFylDrSNwx2dxSqWJlagEdSX2Jb9EXGK+kkB+diudHxQWwmKS5QBfuIUeUqQUzbPgpwpQzuBTRRaz/5YPsgTaRULpEUrpwI72D8SaRkrtKGj04YPtJWizLZYgswuH2ySIn8QK06RJ4gSpyizfczWR5vbHwn193SG/QJZUL+hRZyhnVN1lG9Fjw3qaLNsncYbnGyZ0wtp09Ic8mVLW54NLaCOexbsptmBNqKlOeTzljaN/Ab7VCDNgQ/whG6ONT7raIM2AdaxVi3NgeZIi1jzNl8C7fKhj7R0/CELdJRIC8h39cFPtG7pQz7Y0P5x9cFWGu2voR812lC7oYO2gqzY7PMF5Lv6+oh2dkAbatA9w7Yy0DFD+TP2mkZ9M3FU39EoD3Q50BxpCf3iaJAH7nI1CVuATga+ADRD2hnF5UOHwWUihgmrTdIW2MykYQtiGxwy8CC4EORDVgxXZxgmbAFvC+BpbAP8DQoY0rI1GGTFcFGEYcI+wbBx8KDYNGyBhj3lJsGhgLc0FDQJ4cRtah1kBy+KTVMgHa+0TcAjaBPjZsY9zYHmSAunSFNwpBVY1DQF0N1wlOYSmUvwNiFdwj1iXIlopl00XjNhJqwj1dZEfVBT9+uM3qaggTalXFm6T0GZaVLgDoCbmNKuBXRjSB1sAb/cpaRLGWc01tQ0R6q6/tqrxxx6wF/3HHPda7UVTepId4Z9J5qa2C1N6w5fIMWblHD6tWVH2kJuDPuCokkJl8KaMEphed+mjsu0a0E3rbsh0AIXc7rzViPsS7MvO7KnwzJYHosmJVzK1XTYxloAtKnjMmcl3liJO7s00Acp6VIIwM71OcKNyz30H3cO38AntHSccl7AAY5snFDWxdKGFHBbdFOVK/iM+SK/LWwQFomv4rdlXi8fFr/9zf6xwfLzfFH83dZ4tGGNC45Uyo00RmmhhNR8t/s/kmK1MQ==
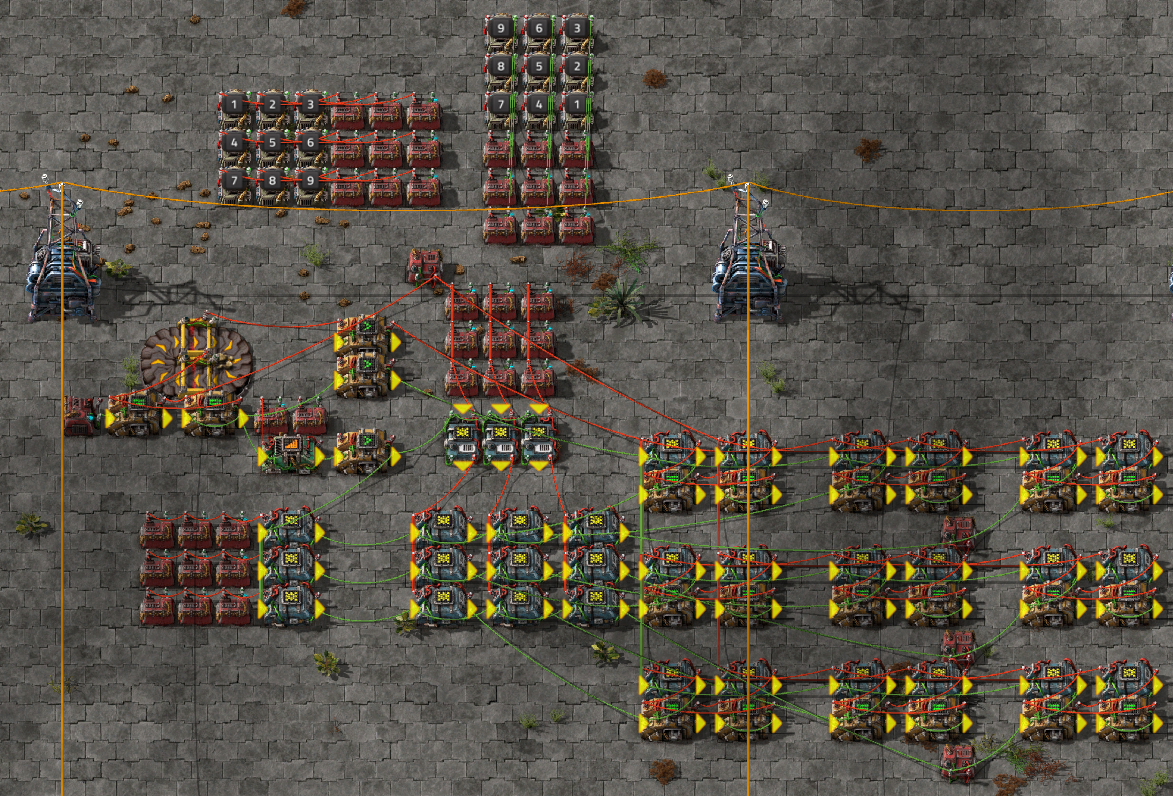
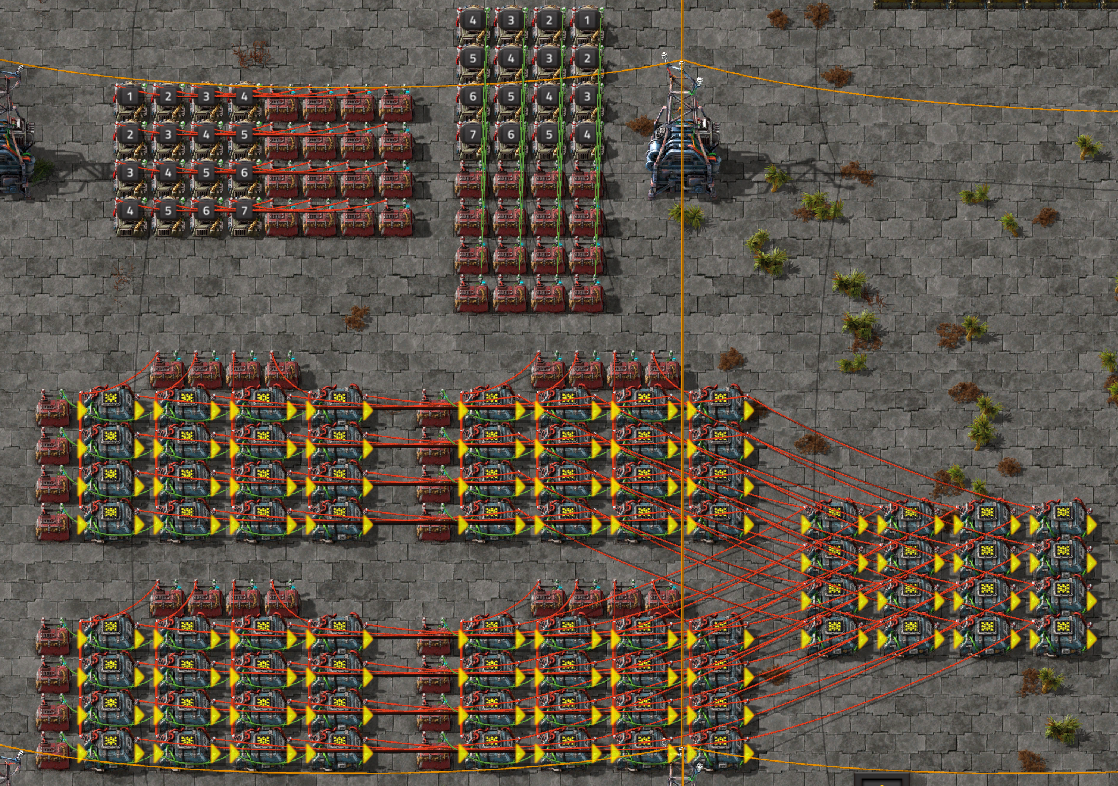
10x10 * 10x10 matmul
0eNrtfdtu5Tiy5a8c+GnOwH0gksFbAWc+ol8bjURe3F1GZ9nZTmd35zTqA+Y/5svmS0ZaXJTkXd67rNgu75IoFFCpZVK8BC+xGJuK+PfVh8/fbr483N49Xv3w76vbj/d3X69++NO/r77e/vXu/efhb3fvf7q5+uHq/cPt448/3TzefvzDx/ufPtzevX+8f7j6+frq9u7Tzb+ufjA/Xz/z1qebj7efbh6ef8X+/Ofrq5u7x9vH25tSK8D3d3fffvpw89CXeV3LGdr1+P7ucV7Q9dWX+6/9u/d3Q4V9eT7/l7+++n71Q3b/5ftq+pceH+4/v/tw8+P7f9z2b/TZvt58HN74+vS5r7p24/rqL7efH28eDv/6+P3L0JB/3D48fuu7OLasdPkPf324ubnr//r3PrHvQp9wd//wEzL2Tf7y/gFN/uHqv/GHb4O4489/7v/7eZDbQb+ttt/2zfv9cPNpWa/t0V67hb1OqxrtdLTfou33CkbbHO21X9brYFY12v5ov4O23ysYbTna67iw192qRjsc7XfS9nsFo+2O9jov7LVb1Wgf77fptB1fwXAfn+RmIU8LdlXjfXxXM1bb8RWM93EVZhYyteBXNd7HOYsRbcdXMN7HCapZytVkVeN9/ERigrbjKxjv48dPs5Stxa2s76Tt+KqPYmYpXwsbGW/baTu+6vG2aruaf/Nuf/z+/vXMamq7mrx5vwez7GupMau2rK1hvI/zFqu2rK1hvE+sb7VtbQ3jffxcYtW2tTWM9/FjqFVb19Yw3sftDlZtXVvDeB83M1m1fW0N4328305tXlvDeB+f505tX1vDeB/f15zavLaG8T6ux5zavraG8T7OW5zavLaG8T7OU53avraG8T7xg7/avLaG8T5+DnVq+9rK17favLbu85hT29fWPd6iNq+te7xl4msP9x/uv9w/PP6ys0k4xH1HH27+/u3m6+O7seVH+jbU90x19gXVmeG3jFeqb6InX7996IcV1fzSmsIK47NliNYUF998any/+fz5/p+vtfmL1/Y8vHnPv9ze/e21lL0ErTFuHSN+4n5f1PZ8DSN+YhtMWnPcGvp9/NgqWWuWWkO/j5tnfKcd73Ws8OMHdm+0I76Onh83TXmrNcmto+cnZrvT9nwNq/zEiIvWKLeOET++r3uv7fkaRvzE7ha0Zrl1jPiJbxSitudrGPHjjNUnrWFuHSN+/JTis7bnaxjx46fS0GlNc2tf48Foe77u01mwWuPc6kfcaXu+8hGXF9ntYjphtwv+RWUMR+ChjPxsGUstQaP8M+T/6fahSBifV73laPxRMxTXV7df3w2N/cv7z19vnhWI2kCU3nxC/vPH28dXM5SHpLWF5ktcPP7+ato2a/u9igE/Tq9ip53paxjw44Q6Gq1pbA39Pn50jFbb71VM9BPfOzutRXANA37cOhRF2+9VDPhxc2D0WnPgGgb8RL+Dtt+rGPATMz1qrYFrGPATO1vS9nsVA35Cl2WtMXANA36cpKdO2+9VDPhx0paM1ha4hgE/TtKT1fZ7FQN+/FiWnNYUuPIVLtp+r9z+kLzWErjyAQ/afq99wOPLTKCWvX22jIkAPe8T8ahF9RfmS3lelFOx7/rkT7ejXP9y+/D18d3kZPFXRHfz/uOPg7vFfjj6Yt7VoYbU77/cPJTe/3D1P/s37789fvm2uOznhZyXCmigGA0JKHeLBeTaEpBZLCDfloDsYgG1tQfll91Rz13d6OcK5vPNX2/uPr1/+H71XMmyVPS5sd3NLxZQY7tbWCygxna3uFhAje1uiymo6RrbhPJyCbW1C2FGLBWRb0xEZrmIUmMiWsxEjekaE5FbLqLW9qKXXU0zRhbzdWxaS8Xf2j4XlouotX1uMSc1trV9bjkrta3tc8tpqW1sL5r50H98eH/3dXBn8IcPN5+f8Wng6+Whnsv+QjrPlm00ZZu+7GdLsy8vzZxo6fPj+PH24eO328d3DzfvP7378X0Zgse+Df1gPj58u7kec9S/l6w/3X/qW9Q932KnabE5bPHQ8Tdrsry8yfZUk58t3GsK/8UIpmfLnnTqM0GwjnnLePn8YKEHi3yO/qRe809+WPtfV0OYrrLED2ODvWydH4saEXUSMu1IKCmvS1chveUPtZ/uH1/NIbnRXpBfe8dtpx7x7gI+k95//Nvrdd2ox3z1Xddek1/9dNdek199x0U94quf7F495qvvelDenV79dI/KrwRW3/Gk7vjqJ3tWT/a1d91pr8yvfbo77ZX51Xfcqkd89ZPdqcd89V0X5T3q1U93r/xiYANjHtRjvvquR/Wor3y6L2Rxcbm5f2UuS4xb/EtWnC2EF3lxea1fsrrf6mesvqSHYz9jzXyfv8S4zU9EfmPzf23+4/3dTbFiz6Txiykxf/vd3c3jP+8f/oZahlCE/EGnhGOczZOFY3N795f7py3JBy35f//n//5qW1D92JihZaOJ/uYdW/D+7pPeTF9Guv/rC2o+GjvYKL8bevkvHmv/7VeWf9ZgLrSpmItsKm7RpsLPqi77m+Iff/Fz2X+fuw6PrjBRfnjW0Arzy2aQ29XS1tVSUH6M2NCiWXZRIfnGtt2k/FqzoRm0/JPoS52W7CWIjV92Wkr7aWnraskb5RfO7WwqfvFpKV/qtOQusqksOy3lxk5LXvshe0MrbNlpKe+npc2rpaB0btDQoll2WsqNnZZ8Unp/aGgGLT4t5UudluQSxCYsOy3l/bS0dbUUjNJjSjubSljuqKC71HHJX2RXWXZcqh5lmlHcQbROdxpaZH7hHNpPTJtXTUHriamhZRO1rpgaklFauLU0dq4MCo9nlzo1hUvwm9gtnED7sWnruimq/bu1s+9GhYO3S52b4kX2lYXnJtPYuSmK1kNgQ4ts4bnJ7OemzeumoPUa2dCyiVrXjg3JaOG5yTR2borLz03mUuemdAl+kxaem8x+btq6bkpG6y+2nX03LT832Uudm/JF9pWF5ybb2LkpidbjcEOLbOG5ye7nps3rpqD1Qt3QsokLl01jZ4KUtG66G5pDC917yeSp1F7YJwZ2w9fyDZKXHY98t1AIv7kGupg6eUa1va46qc08R53kpV5p3cE0f8uJPXRu4by+Hou3LwlBfHO3NMr4VIF7gbuibwtD/bpZ+fKr5X/8/n5h+2VWvv/V8r/c3i30tuRn5YdfLf/7zefP9/9cVkOY1RB/m3jqUwXpNwhjnWbl59/C41WeVTD88vTqjqW6E9rDLtMe9i20x1sSsbJHHxXPQt+CXi64+y6nFacmxiwi1s3nvpX3vzIzhP12L5wZc25Yari65sO7n97/a1SS6P5SavB8l7wu3oPbXLyHobwv399hFrz7y8P9T+9u7/qyKgs6NiUWn2xnLvLdmxoUDw4li9/TH1x+fP/l5g8/3j/c/u++e33KzyoW+qTdLzKEHBmyxT9QzgI67EN2kSFbfPaf+ebfh+wiQ7b4J9xZTIF9yC4wZHZ58OGZZ/x9yC4yZIt/9J159N+H7CJDtvg36Jlf+n3ILjJki4NFz/zp70N2kSFb/EP9zDH6PmQXGbLFMcFnbvz3IbvIkIUzHM7bzTuct13UOZy3+02Ybd6EscvjsY+TwrVxicEuj8c+czhvN+9w3ppO53DeNnFPyBqjdjjfygozVudwfldLW1VLxqkdzjezaETncL6VbderHc43M4PCGQ7n7eYdzlsTdQ7nd7W0WbWU1A7nm9lU8hkO5+3mHc5b2+kczjeitq1RO5xvZYVZq3M4v6ulraol69QO55tZNKJzON/KtuvVDuebmUHhDIfzdvMO562NOofzu1rarFpKaofzzWwqWe8vvBUZue4cp/x28075rTNKp/yNkBtn9d7Fm1lkTumUf1ffW1XfTpTO1FvZVrzeIX8z20o4x+G83bzDeeui0uH8vu9udt9Neofzzewr+RyH83bzDuetdEqH840obzF6h/OtLDKxSofzu27aqm4Sp3c438yyEaUz9Va2Xq93yN/MHArnOJy3m3c4byUqHc7vummzuinpHc43s6/kcxzO2807nLe+Uzqcb0R5e6N3ON/KIvNW6XB+101b1U3e6R3ON7NsROlwvpWt1+sdzjczh8JCh/OTwzC/Bk/cfz46OeLCjvsLdlzjwvt4z9PCnssFe67yjn6860vDK8QLdl3j9/xoz0O3sOfhgj3XeJQ/3vOFsQYkX7DnKk/xx7tu1dFE3r7rOjf8x/u+1Mm5uej+vti//gnVFmRh17vLbvCLQxcc77lf2HN7wZ4vD3lwouPLvZjLk45fjOm+teu1f9w89F24uOO1sNyHeXzzAfuFwF4+Zs+4uTv3GNMdO8OEtNyFf+OyNEdludzrt2lclvaYLKPCHXfjsnRHZbmQxc9cLsuFA+P9UaPlr69uv767f2Is/oVIFH6oG59ecnR6LXcQ3bo69kdludxzc+vqOByV5WITdmxdHcejslzu67h1dZyOynLx8SW2rnvyUVmmM3xwy/Z9cMes88Et++WAjV4OSJ3aB7dv5HfdZM7wwS3b98GdrM4Ht7RxdSI5tQ/uZlaY6Hxw72pps2rJq31wN7Nogs4HdyvbblT74G5mBqUzfHDL9n1wp6zzwb2rpa2qpdypfXC3sqlkc4YPbtm+D+5sdT64G1Hb2al9cDezwkTng3tXS5tVS17tg7uZRRN0Prhb2Xaj2gd3MzMoneGDW7bvgztntcflRqaQ6zqdm/Jdc29Uc7tO6z65Db3kOnuO/23ZvP9t1zm9E/dmtl3R++BuRkZe6YN7102b1U1B72O6mWUTlX7KW9Hf6Rwf3LJ5H9yuy0of3Pu+u9V913R6H9yt7LvmDBfKzcjInuOnXDbvp9wZp/RT3ojyNqL0wb3rps3qJq/3wd3Mvhv0PqabkVFU+ilvZetN5/jgls374HYmK31w77ppq7rJdnof3K3su9ac44NbNu+D21mr9MHdiGKyTu+Du5lFJkof3Ltu2qxu8nof3M0sm6D0wd3K1hv1PribmUNJ7YM7/v59cB/3RO1sVnc8/P47ftwPtXOd2vl4WIHzcTnRc6N2Ph7X4Hz8VNetuuthDV0/sdCdU8/3uIL57k/0XNQe58MKPM6HEz33ao/zcQUe50/1PKh7HlbQ81OzPapne1zBbI8nep7UUQbCGqIMpBNdz+ooA3EVUQZO9F06dd/DKvp+YsqLPrBGXMOUP8FnxKqDS8R1B5dwoo+rEdbedX1cjbiCuBqn5rtX9zysvOdBHVEkrDmiiJOo7nhcd8eTOpRK3EOpvH0oFbc8RPM4YGEfsAsMmO/UsW/iHvvmQJZGLcuwy/JAllYdRyjucYQOZOnUsgy7LA9kKeqYTHGPyXQgS6+WZdhleSDLoI5vFff4VgeyjGpZhl2WB7JM6sBYcQ+MdSDLrJZl2GX5VJahUwcZi3uQsQNZGrUswy7LA1ladcC2uAdsO5ClU8sy7LI8kKWog9/FPfjdgSz1gQTDLssDWeoDCYY9kOCBLKNalnGX5YEskzooY9yDMh7IMqtlGXZZPpXl8jjoswCXYfMBLl00ugCXYf/ybqNf3i0P7T5OitjIR1PLI7bPAlyGzQe4dFF0AS5DG98lLg+sPkqomRUWdAEud7W0WbUU1QEum1k0SRfgspVtN6sDXLYyg5YHN0+XOi1dIsClS0YX4HJXS1tVS8mqA1w2s6m4MwJchs0HuHQLg7nnxk5LyyOb59ZOSwsjm+f9tLR5tRTVAS6bWTRJHcGxGRFlXQzQRjTT8uDm+VKnpUsEuHTZ6KI37mppq2opW3XI01b23HxGfMJmZCTKIKCtKCZ/ThDQsP0goAuDm0/BG3fVtFnVFPUxT5vZd5MyeGMr+27WBwBtZA5J150T4DJsPsClLI5wvh+bNq6bRBPUPbW2r7hzgjeGzQdvlE6UwRvbUN7SeX2E1GYWWVAGuNx102Z1U9QHuGxm2SR9gMtmZJSVAS4bUU+KIOfmUuemSwS4FGOUAS533bRV3aQJ6N7aucm4cwJchs0HuJSlQd1tY+cmRYRz29q5yQRlgMtdN21WN0V9gMtmlk1SBrhsZevN+gCXrcwh26njPObff5zH4/GwxBp1x9Pvv+NyouNWHfAvryDgXzzRc32ow7SCnocTPRd1fMu8hviWp7ru1V1Pa+j6qS0uqEP+pRWE/Esneh7VYR7TCsI8ntrjknrM8wrG3J3oeVaPeV7BmJ+Y7YtDVucLzvZXjfYnTh/oMK+961Yd3zKvIr7lqb47dd/T6vsu6iiPed1RHmVp3OpZ19Paux7UYR7TqsM8ytLA1bOe55X3PKnjPKY1x3mUpWGrZx3Pq+64dOp4iXmPl/j28RJFjHrA0j5glxgwqw7KmPegjAeydGpZpl2WB7IUdVDGvAdlPJClV8sy7bI8kGVQB2XMe1DGA1lGtSzTLssDWSZ1UMa8B2U8kGVWyzLtsnwqy+UB1INvfF7KUVkatSzTLssDWVp1UMa8B2U8kKVTyzLtsjyQpaiDMuY9KOOBLL1almmX5YEsgzooY96DMh7IMqplmXZZHsgyqYMypj0o44Ess1qWeZflU1kuD6AeW+fq+agsjVqWeZflgSztGQEu0+YDXMosKPqiAJdp//Juo1/eBWV0wtTGR2XLo7XPglumzQe3lKAMTbhvKJvdUKIu7l4rG0o6I6hc2nxQOQlZF1Ru31C2uqEsD1qfL6WCLxExTRYGrc+NMbhZBPdF4cD2DWWzG4rTBXJqZcHIGYGc0uYDOcksYP2iQE77hrLZDSUoI/C0sqPEcyLwpM1H4JGYlBF49j1ls3tKVkaXaWRPSWdFTknbj5yStJFT9j1lq3tKsudEBUnbjwqSnDIqSCubrigjXux7ymb3FK+MVNDKkgnnRCpI249UkKIyUsG+p2x2T0nneOFP2/fCn7LSC38jm27ulB7m9z1lq3tKNkrv6a0sGat1kG2637+D7BMeg7NTd9z8/jt+wndsVnuJvsCIK1wln+q617oGv0DXl7sGP+E8Ngf1oJs1DPqprkf1oJsVDPoJz4JZ7SX6AtP9Vb1EZ7WX6Av0fLmX6OM9912n7rlZec+NerabVc9236l9RF9gtr+un2TfOa1r8Av0/VVdg/tO1F03a++6V894s/oZH7TusS9CYl/RPbbvorrrZu1dT1r/2Jc5tX1/vfme1T036+656bQOsi8w5q/oINsbo+64WXfHrdbRNDu+O5p+U0fTfnng6HHAun3ALjFgovVm/YYrbB3erP3yoNejLLtdlgeyDFpv1s3OS3NUllEty26X5YEsk9abdbPz0h6VZVbLsttl+VSWttN6s252XrqjsjRqWXa7LA9kabXerJudl3JUlk4ty26X5YEsRevNutl56Y/K0qtl2e2yPJBl0HqzbnZehqOyjGpZdrssD2SZtN6sm52X8agss1qW3S7Lp7J0ndabdbOyTEdladSyNLssD2Rptd6sm5VlPipLp5Zlt8vyQJai9wxuzOY9g3vnVZ7BX7xo9y+mVvbFlHfLY+Kk38dP2q+6aErZR0QU9d7B33hTMRfZVJY7O+5am0JZ5X//t913fzefJXpZfMxJrrEZJEblgn/X3JvV3LL4DJZ8a4vGqaIUNLPtij5KwRsTm0tEKfCyPCxMa9xYgiqQw66WtquWoj6QwxtvKu4im8ri01Ju7bQkWRXrohW17ZeHSmnttOSNKhzIrpY2q5b84tNSbu205HURU5rZds+ImPLGxOYSEVO810VM2ffc7e65i39byq2dn70iaEprxwGfdIF3mlFM+YzAO2+smS4ReMcHRRSR1k5MweiCE+3qe7PqOywPJNK1dmYKThfAqRXdFOSMAE5vrJvCRXSTXy6g1khyCLogV7tu2q5uiroYTs3su+mMIGBvvO/Gi+y7yw9NprWDd+x0gcD2fXez+240y5dNa0fpqAjA2Nq5KTpdQLlW9HeUMwLKvbH+vkRAOR+Xn5tMa+empRHrzX5u2rz+jmcE3XvjfSVfZF9RRCVs7lygDEzYivJWRK23rZHkpYHr7X623LpuUgSut62dm5bGrreNnZuSqOM8ut9/nMcTsQSSV3fc/v47nk50XB/r0K0h1uGpMdfHOnQriHV4qudJ3XO76iiPPmX1dLdrmO4nup47dcg/t4KQfyemezbqMI9uBWEeT/Xcqntu1x3gcnHE6njBnr9qgMvFIavTBWe7Jtzfqfnu1VEe3RqiPJ7qelB33a48wOXioNXpgl1/5QCXWR/q0K0g4N+pCZ/V8S3duuNbhqVxq2ddt2vvulHPd7vqAJdhaeDqWZxHt+Y4j2Fp1OpZx+26Oy7qeIluj5f49vESQ+fVA2b3AbvEgAV1UEa3B2U8kGVUy9LusjyQZVIHZXR7UMYDWWa1LO0uy6eyNJ06KKPbgzIeyNKoZWl3WR7I0qqDMro9KOOBLJ1alnaX5YEsRR2U0e1BGQ9k6dWytLssD2QZ1EEZ3R6U8UCWUS1Lu8vyQJZJHZTR7UEZD2SZ1bK0uyyfynJ5APXY+rknHpWlUcvS7rI8kKVVB2W0e1DGA1k6tSzdLssDWYo6KKPbgzIeyNKrZWl3WR7IMpwR4NJtPsBlWB4UfQxnaNv4hCjYpIsB6vYP77b54V1YHrF9FuDSbT7AZVgehX0M4NjKpuKMLsCla+KzxDCLl74oeuO+5251z10e9T251vYUUQe4bEZEXhfgspVtN5wR4NJtPsBlcFEXvXFXS5tVS0kd8rSZPTefEeDSbT7AZZBOF72xEZ0kRh3/s5UVJlYXvXFXS1tVS+LUIU+bWTSii97Yyrbr1fE/m5lB4YwAl27zAS6DRF2Ay10tbVYtJXWAy2Y2lbOCE7rNBycMvtNHAG1lEnmjjADaCLnxVh/gspk55JQBLnf1vVX17UUf4LKZZeOVAS5b2XrDOQEu3eYDXAZNhPPWSPLiCOf70XLzuimfE8DRbT6AY1AEdTetnZuWBnU3jZ2bglUGuNz33a3uu8HpA1w2s62IPsBlMzLyygCXrWy94ZwAl27zAS5DiPoAl80ssqQMcLnr783q73xOgEu3+QCXIXb6AJet7CvRKANcNqK8FRHObWskeWmEc7ufLbeumxRB3W1r56bolQEuW9l6gzrOo6w5wGWIUR34TtYd5zFEfbRDWXWcxxCzOvybrDrwXUj6YIey6mCHIRl1MCxZefi3kKw6BpqsO/xbSE4dF0lWHQcsLI1ZPQuGJSsPhrU0avUsMpKsOjJSCupAO7IH2rlAoJ2kDw4je3CYA1nqg8PIHtDkQJZZHYRD9iAcT2WZO3XgCNkDRxzI0qiDHcge7OBAllbtoF92B/0HsnRqp/KyO5U/kKWoHaHL7gj9QJZe7bxbdufdB7IMaofTsjucPpBlPMPhtN++w+mc1A6npZGf9GZx7hc5nPb7D+Hb/CE8dt0ZDqf95h1Ox86oHU43sqnEzuocTvsmrgnETu9euJkZJDqf3Lta2qxa8mqH080smqBzON3KthvPcDjtN+9wOnZ698LNrLCs88m9q6WtqiWjdKjcyJ5r9A6VW9lTjD3DZbnfvMvyaJzO4fS+5252zxW1w+lmNhW9R+VmRBR0Prlb0dzxDIfTfvMOp6NJOofTu1rarFrKaofTrey5tlP6Cm5k07XmHIfcfvMOuaO1eofczSwyp3c43YyMROlwelffW1XfVutMuRXdFPQOuZvZVuI5Dqf95h1OR5v0DqebmURZ6XB6101b1U2uU/oKbkQ3OXOOQ26/eYfc0Vm9Q+5W9l13hnfhZmQkSqfcu27arG7yeofTzSyboHQ43Yr+juc4nPabdzgdXdI7nG5mkWWlw+ldN21VN0l3jsNpv3mH01GM3uF0K/uKWKXD6UaUtzi9w+lm5pAoHU7vummzusnrHU43s2yC0uF0K1vvdG76+u1DnxedfcYLK8USny8lvaiUISoQS5l7Wvx889ebu0/vH75fPVt2PsNFRdy8i4q4PML86IIhNLIJLAwwP8on7qpzo6rT2zNcVMTtu6jwTu2ioplNRXQuKmIbxGJhZPnR/8K+5252zw1qpyXN7ClR7aKiGRElnYuKVrbdfIaLirh9FxXL48qn1k5LC8PKp/20tHXNHazaB0Mzi8ad4YMhbt8HQxCdl5NG1HbwaocEzaywoPPisaulzaqlqHZR0cyiSToXFa1su/kMFxVx+y4qYqdzUbHvuVvdc6NRu6hoZc+NVumiopFNN7pzXFTE7buoUASS71o7by8NJN/tx4HNq6ag91rSzLKJShcVreimpHdR0cwcyue4qIjbd1GROr2LilYmUTJKFxW7/t6q/k5W6aKiEd2U3DkuKuL2XVQk0buoaGbf9Ur3C/u+u9l9N+i9ljSzbKLeRUUzMkpKFxWt6O98jouKuH0XFbnTu6hoZZFlo3RRsevvrervbM9xURG376IiO72Limb2FVG6qGhEeWevd1HRzBwKShcVu27arG6KehcVzSybpHRR0crWe44DiLx5BxCp0zuASG0ssdQpHUDkXTFtUzGl7hwHEHnzDiBSp3cA0cymonQAkZtQ26nz6s/9m5lBQecjY1dLm1VLegcQzSwapQOIVrbdcxxA5M07gEim03k32Pfcre65xqhdgrSy5xq9A4hmRHSOA4i8eQcQySgdQDSito3eAUQzK0zpAGLX3JvV3HoHEM0sGqUDiFa23XMcQOTNO4BItlN/7t/KCrNG5yNjV0tbVUvW6r/fb2bVnOUEIm/eCUSyovQi0ojmtl7/tX8ziywonWTsummzuinqHRw0s2yS0klGK1vvWQ4g8uYdQCR3hgOIVhaZ0zqA2HXTVnWTs+c4OMibd3CQnNM7OGhmXxGlF5FGlLfTOoDY993N7rtnOIBoZls5wwFEMzLSOoBoZes9ywFE3rwDiCRnOIBoZZGJ1gHErr+3qr/lLAcQefMOIJKc4QCimX1F6wCiEeUtZziAaGYOaR1A7Lpps7rpDAcQzSwbrQOIVrbe6dz09duHPi86+8uv9qWIxZpnS/Hdi0qpF8/7Uq6v/t43ti+kf+XzzV9v7j69f/h+9WzZ5kVlGyOawid693D/4f7L/cPj8W9D7TAjHm7+/u2mH8y/3H5+vHnAYH8tU6SMy+3dp5uhOYPAn6vQvaBCM1y+VdXYT5J/9lN2SPiTuTbX9tr8+bo8lUfXP8r4ZMuj7x/D+GTLY+wf0/hky2PuH003PrryaIYKjJ2eHZ+HOoxMz47PQzUmTM+Oz0NNJk3Pjs9DXbabnqU821nH8NwTCTzP+obnfqfE86x7eJZSvp31EM/9qsDzrI947kcPopv1Ec++1OtmfcSzL/W6WR/x7Ev5btZHPAdTnmd9xHMo9cpQZorTs+mF6AqwQ4Ktz8MMkgL8kOCHZ5kkhOdQWtEzi1FCeA58TkNLSysEvS+tG/50HUvvhz9dR84iO0kIz5FzSiYJ4TmWHvswSQjPqdTl0yQhPKdSV+gmCeE5lXqDnSSE51TqDTL1Hc/ZleehLpNZ6ABsZKnDGMTSipAmCeHZ2JJpSL82nI3RTLKIZRWURkU3CQbPg2YB8JNk8Gw48WKcRINnY0vtMU+ywbPh1EtmEg6ejStSSG6SDp6NK5UnP4kHz4azMmG1p/psh+dhMg1/us6lbjwbMRXYIcHW5yGBoK9RxlcEAClD2zNfL/1IMyBSwfB+6chQ8zVHaqhseLblecjka4IAIGWQQy5F9c9DrjLDhlKus6/Pdni25bnPxGneAwFAyrB2TCeYNACDngMYZnEukuufh/fZ3kGmOdZnOzzb8jxk8jVBAJAyzL/MzTUgF18fRiTn+myHZ1ue+0yhqwkCgBSMT8cUDANXRS7btqnAAtgChmy+pgjAkIKC+nzcyTtIPHA/7jDbOjciC2SJ+r9zFQ1IgEqaxXueaRB9rKVgonZhRBbIEg05/ZgmQCUNy7zfiDwQZnUXmRNyj7XVWPjdhCyQJepzpm5ME6CShtXYZaZhAFJtNeSc/IgEqLwH4XK/NsZywy4Ivc1Vfw4DPGxJApRmOwxRrqXk2VZExJlorJ1tQEScWsbO9yAizi5jw2y3KchyshgbZ1tUQZZTzLhuthkVZOt8cfP9qCBb58ugIcedpyBb54QruxJ760p9lUGk2V5tHOaxlA2hIBuL1hvQtO9gM8KW4oimDQbbWY/CDNk6QwTzWjgHgWydLzLMclvnmQyzfEAlzeK9PKJpezJFO/f/Rzuhho3U+iAJY0bU5yXZwl6HvcwRTTsbWt/vG2ZEFsgSDaXYMU2AShpmnVBmUPfGU9aS8F5FkLWv7+XZLomtExugI5q2Q7SpR2FEFsgSDTXEMU2AShok6POIpg1zKNuiBrQahMJ4StBDZnXleMjMU2bez3ZXtKnfz8yILJAlGkqxY5oAlTTIzFNmoCcmVFYLmdX15yGzUN/Ls50a2zd2Z0c07dVoU4/CiCyQJRpqiGOaAJU0yCzkEc328gCZBcosQGahlgKZOUoiFGqe2DI/3/ULcarrL0BmkTILkFld7wEyc9QIoFWGZGhAQ86KwB36/5eWQWaRMgt5rjsK74qUWezmuqNQrxhGZIEs0VBfHNMEqKRBZjGPaKZXImQWKbMImcVaCmRGkmMKjYuUWXyicyJklsyILJAlGkqxY5oAlbRyFKKUImQmFUFmkTKLkFmq7+W55kqQWaLMUjfXXIUxkgyiTUCWaKgvjmkCVNLsXMclSClRSglSIo8cUJ9KamUK30xcjcnPdWOCJLwdkQCVGrDiElcc6KWtu1RC30lDoU2hRR2RG2m+AS80JIYGBHDUt4X19WmlFAFi/wpZI40ryNbVmDGaY1pBeUR9O+vKAWmzdcXl9CRngl4xI+pzVvYEemZ5Chn07pSzIjei4T3HnBg/nksGnTzPWZAf0ZCT52bwLMuVOujdeU6MJleABbOyXHEWXMp2mTkH5IbVSzTpRmhMaDVHNOk46N0euTlKU5pFmp0QZ7ntiszymFOAShp4gQkjmvTfUK9F7WgnDBfWUBIFca0MqK8hVUuDRU4pfTB2pinR+h6lEVkgSzSUMuUUoJIGWff/L22BoYIsb0DDe5S1gawN+2fCTG9Cm0L/OaJJG6JNPXIjskCWaKghj2kCVNIgQRtGNGnDoWyLGtBqmmMoQQuZcf1Bm0I3OqJJU9pirqn2FwuZWcrMQmZ5yilAJQ0ys5RZMe6QxQ5oeI8ys5CZ43yxYaY3beG0vf5zRJM2RJt6ZEdkgSxR3zZy4QEJUEmDwcpVSWTkZJkOMnOUp+tmmnKo16J29MhBZjwko14gSzSU6cc0ASppkKejrJ2b6dvhXwtUaoDMpLbMo0yucFdkxlngwkxv2sLLhfPMxZk2tIWlk1+jvUCWaKghj2kCVNIwzySMaNKGQ9kWNaDVhaVXWx+YuKu7hkBmwr6LnelNtKlHaUQWyBINpUw5BaikQWZCmYGJW7JtCybuyGLR+j4ne1TYNvUmtCm0oSOadCPa1CM3IgtkiYYa8pgmQCUtzzTlUJpFmWgnuLelzcGCbbtqK4V5btCijmjSqUO9Q84JCVCpAZLwlAQYtRvtqTg3kolbH3+JaLSwPj+D2DKw30PEtgT3DGL/QjHtsi3gpq6OQ2GjgeMANurq+A1/hZ6uaQKE/sHs5+qogKnaUMvEHll1XIChuMo6lLMo9wKw2AEhJ1is4ykEeaCnLZEAlZwWOTnuYKqDfrdEAlRywuzMswzyQIdbIgEqOQU52aOI0STfRR6gkrOYrNmjIQ+0vSUSoJIzICclD4Y7sARLJOOpHNwBvKDkLDqcbAbIVcnHJzocRs9B+zqimS4Gw7W0vxTk4pRmkWZH5KqswYUdzzIDEqCShl2YFlBb2G/V0wnjkDhGMK5astiCXOVSCeuocikw40GHO6KZRgcztrQFob1AlmgoZcopQCUNsk4cB5hwbebYDjy7z8n1BwutzbV/T/Q7rK+WrNnC/DpqbTBqS6sp2gRkifoaeLKxMMK6OpoZEsxpRDOtDe5tyb3R3h5RghkyqwwJZtZBhzuimUbPRWZ5RBbIEg2lTDkFqKRBZpkyg5HV0S5lwdJdZUHg5a7jfMlP9HsuPwzVdmbklDGtLyWbMU2AhjSwBTABRzTxAgcr6vB/AbJAie/N9Tva2yP+ngTO7siQ0KZeP3QjskCWaMgZxjQBKmlY711ky+ZMADX1pZgRDaXwV6uB1yNnaTVkRn7turl+h9aHnnZEk9ZGe3vkR2SBLFG/h1UpDWwdqKThhzjaVB1YunBU0Io+jRI0dqbRHXj58H+02hSZse9GZhrdlZ8nyaHRJiBLNNQXxjQBKmmQma39C8jJX/1g7XX8hQ4t7HPWHs31O7Q+tLYjmnQ42tQjPyILZIn6+uqIWcjMsAZrZhp9KM2iTLQFTNzRvuTAvYWcCIwA2t4RTbrfgW2LmZAAlRqgi21gDRE5OXvAr52r7URv6++qsCcfItZQfoCltcmVn11d/Q1WnuQEqr+llh9iaQty5edXx1EBb51yFlTLRMvIk/FvjygXMM5DxBrEzUshYstgtXX8pRlv9IhyAQOs/KUg4e9rrjBAWl8dGKCjtdf5bsZtChIycbzRp9kxpwBhVGCZdWScDrZYRwur83bGggqS2iPYaZ3nXIKd1pEdojRwIkskQCVNZnypIKkyA8d0tBKjNKDyHtafj0zDzk5brAP/dOMv7vhRu0oX9l3nuRfAojug8h5WI23NKA2opKUZBytIRukWxsJx8BiV0PE9aIRQRwVjFLizw/Zb2VpBUqUbMEa0GaM0oPIexihwjGD7dbToOvzsXXldQVKlC7uwCxwj2IUHVN7DGNFKjNKASprMGGBBUqUbMEZk1CgNqLyHMaKNDKUBlbTCFWsp1U5kiWS0GiFPXx/XA1i6I0tHTSNXdIWlk1UWJDxbuFg4H2UGJHWM4pzzgQmCrTmiibu5wsRp+SrI1/0FvNyR7xbkebYfUC/ROirg7FLHDyzd0YLlwNIrr3Pg5Y6c3RUmHuuNEVwfGe+MYN8NtZ2QLu3QDtblygBd4d5kzWgvkCUaSgljmgCVNMxy2prRiv49zgkwcamjWfh1Yv/SnA+CJYLXOaKJ5aFNPYojskCWaKghj2kCVNIgQfLkAU0sbyjboga0Gvza0SrtwKiFzB8sEZzPEU0MEG3qa7AjskCWaChlShOgkoYZSSbuYLGWWBF2hsRZDkbtyKhd4dCVK8JiPfA6RzRjebjM4Mia0SYgSzTU58c0ASpp0EBkzQ5sW3i2GMq2qKG0bFjFQr7rCoeuXBF3FgYG6IhmfBCMWvgrMNoEZImG+qacAlTSMM8y51kuF6BqHzDPuALQpj6tzLMBTXwQLBEM0BFNfBBt6lEckQWyRH1OnmUEbFtSLXOYZ0IOLbh7UFmegF8P/8ddK3Bo4a/HAg4ttCCDJYIBOqKJD6JNfQ12RBbIEg2lyJgmQCUNex1Zs8AKLqmijJaVeYbW9zkpMzPng2CJYHmOaOJ8aFOP4ogskCUa6pvSBKikuRkDFNi2hbZttLdH7Hvh0KkiSMkktiXMuKLAmi08JQ9IgEoNYEgmsQbMF57ABDxZaM+Sck2QrFlglZ7SCmJbysXBMWdB7C3uSBwgslEBp51KASKLFbDYMSdRIDJPchZU7/rJM4g1gNNOpRREmYHFCnmrlGuFZLgCm2pllQX5OkMEM4TWV8HtBpGaZmessiBf5yBuPojImFOAMCqwtwrvQQgsrAMqaTJjlQX5OutgfRXahVEaUHkPuxQtrCgNqKSFGassyNdZBzut0PaL0oDKe1h/5N4oDaikpRmrLMjzVxopLJ28HKUBlfewGn2VdUZa4YNSWDpZZUGe50aU1qdxHMDZhZwdpYE5WiIBKml2xioL8nUmg7MLOTtKAyrvYYzI2VEaUEmTGassyNcVAM4u5OwoDai8hzEiZ0dpQCUtzFhlQb6uHHB2IS9HaUDlPYwR+TxKAypphaXXUhI5nyWSkQEiT8+luB7A2YWcHTUBIWdh6eTs+Ld/z41oyMkxAtsWMmoJc84HJgi25ogm7iZg1EJejvd7xP6BQ1dGBp4G1uWIJg4m4MlCJo73e73Jvoc0Y0/gVGBBjmjiRFJ4Mi3IAp5cuY3gbsXwf9QALiy8kyGF75LpCBiu0EaN0nrEWQBbc2Ul4CrgIY5oYiUCe7LQ1oz3e23BHsU5gwCvAEtwRDPOgDsSw/9RCpiqkP0KmOqo7cFUhTcmBEx11OHgpkKOKYWNVl0MNiq8BwF9DV3siGaaGfbd4f8lJ/pHW7Pg5sOoRcE/hdxUCuOsmhI23FH/gVUKWSV0JPSfI5ppQ1hmh/+XnBg/skoBOxTaB/HXHrHVsLcKmSPy9IizDpzPd/WmeHqSs1wi521x2D99V++RYx2R5SFPj3h/HDZOTy7lYdWcchbEG+JgVlPOss/zJnkXn+QEolUMeaDxCkJbTL3VbmfasKBA66sH0/G0JHowHW9qmsy0YUGBjBNv9GlhzClAAuSRFpnmkRaZFmbasKBQe4S7AJ42TpQGVN6LSMtMi0jLTEszbVhQGOUy7BqeNk6UBlTey0gzTMtIK3PJ226mDQsKVbqwTnreGkBpQOU9gzTKGtbJAZU0O9OGBYUqXVguPe2YKA2ovOeQxlHBrYEBlTSZacOCQpUubhR43nVAaUDlPYwRbw2gNKCSFmbasKBQpQv7p+d9BpQGVN7DGFmOkcUYWY6RTTNtWFAYpYsxchwH3D3wro4Dxoh3HVAaENLAOD3trcgDPWaJBKjkNKiP6wH3EjxvPqAmoJLTzrRhQaFKF/cSQpWnwzg4jhhuInjeKBjQkMYRKx/JuKIRKsojKjYWIXJIK/VhHMhwCwp1VHCfwfNOcEGhjqbDOIiMqG8LmTFsLT2qksA4uG5E89qL5Dl+uHXspX73AlmT/XrcQfbk5R5se6wP1mXP28oetxs82bYvbJtWYo/bDVMa5jxvFqMvPWL/wJo9OTTadO159wBtAqppDjlr2vy9Il2OA24We3Jh1NSXQgmCNXtfewQJ8nafx32G6T3IjPzaF/bL+8JoE5Alciizps1q8OUjLMoMdx18/RKpsN/6nRHuOkxpkBlZM1rfI65GsFhPLuy9Z8vcDKURlXYKkUNaqQEyoz0SfQEqZUIf8a7DgObvYYWT06JNfU5KF9zUk6mi7B5xnsGC7Mk/PW4We/JWD3vy9B5kxjvIHjeLPW2VaFOP8ojmaZAZLc9oU4+4u8ES7MlU0aZrH2vtkFI0Y5pDzpo2f6/ILLJlmGehficW2TJHZJFW2gKZkbd68F1P9ou+9Iiyxi0MT/ZbkRtRaacQOaSV9yAz2tbQFyDUUOzC9ds2cOHpPciMXBgt7BHXJriwp+3XF/tu/RIO9y48+a4HM/b1qzrcwpjeKx/TUS6w/XqyXw+e7Mlw0cIeVUmkJzkxz8iTPe5IeFrFPHjyWAp4sidP9uDJnjzZw2o7IfSdzNiDGXv+Nu9T6W391g99oEUJ/177XGtPT3KWTwTZB/DdMScRv0kEw/W0xeLfHrEGMFxPhot/e8TxA8OdchbWVWsotbMtsFWGrn6j2M1yVsRvE8FwA+2R+CtYZUEy45hEPGkE/FIfuoo8UCQKM45JlCY0lJnGnAIkQBFpmWkRaZlpacYxiWg9R2k9t+n43rDGAm/QojTwSEskQEgz3YxjEnE0UVqfVtgFSgMq7xmkOaYZpDmm2RnHJKJ9MBTOTpaO0oDKew5plDUY/IBKmsw4JlE2Ixre4ziAwQcyeJQGHmmJBKikhRnHJKqfn4LBBzJ4lAZU3sMYkcGjNKCSlmYckyi7EQ3chmMEBh/I4FEaeKQlEiCkFc5OjkmUZUTDexwHMPhAlo7SwBUtkQCVtMIH69e5GBXycuQBKjmxHrgaUVOfxvEDgw9k96FwdltzljEKI5LrSOsdyu7TOCq2cL48oqFMSh63gIOr7QTiXgCWiDQ7oTy951BKzTkvs3DFomUC7gsHV6WLceAvhQEsPZBfg132iJIHinVHcd28FPDyQOYfCvd2ZU+uyI+o9KHmdEgrpUDytBmjn0ClLZCu1PrkyXuY847jVxg17wsH3BcOZPehfNzuEtsCxNvDyIM0IXJIKzVAgmS4aBNQKRMSJDcNuC8caLHG+2i1I7IoEzWAXwfy8gBGHci2K5IRlfqEyCGtvAeZkYmjTUCldmENjsjivVIKfC2Qe6P1fRplBjt0IGcPElmDm5A3Iyr1CZFDWikTMiPbRpuASpmQGRl1gB060IKMNvWI/QPbHsuErTnQYo2ye8T9DPbkQPtuAL8O5NcB1uWpBsjMUy64ZxxoT0a914E8OeA7vikN84x2aLS+R5QZ7MKBlmC0qS+l1g4pBTemOeSsafP3ILNA6eI7vlA9DYB7B3LTAO4daO0NxSUBbbgBbHt8D/c1Ai3IoTgpINuuyI+otLPmdEgrpUBmZL/oC1CpHTKr/grwHd/0HmTGuxxofY8oM9y0COTsKLsvpbpDgMyiHdMccta0+XuQGTn0gBxQyQkp8d4FWtgjSgmMeswJDh3ItgNYcyBrDrgxMZUCSUTKLGL2kIkHfI83IfSdN5lDLC4tKMFYessexdIHalHcbgip+n8oHIXtBN8N1RMF7iwEMlz82yP2Dww30NqLf8HkCoLkad/Fv2BWFQkQWo0bu4F3dPFXoJKGGUnbL/4KhDTcKAi8Q4C/ApU0yJo3GPBXoJKGOZgpa9waGFBJw6zj/V38FaikYXfjDQb8FaikYRx4awB/BSppgyQib+xCQ/c6rhvRkLOmJeg/yrqgun/i1kDs3JjTIq0ih1JqznmZGWWWe5UB9wsiGTxa0aMyRhH3CyLv9kIL94iePAriXhdx22AqxaKUIl20vkd07oEbBZG8POL+buSpIOJ+wVQf3KV0xeoQcX838r4pWnEdjRnRPC2ghsDaIV3y6wiuH8n80aY+rdYOCRoZ0xxy1rT5e5Agv+OLuM0bTfWJ0rFljsgiDW2BnT2SX6NNPaKswdIjuX7El3SR9xIqCiMq7RQih7RSJmRGZoy+AJUyITNb/bX4J+9BZuTzaFOf0/A9yIwsPZrEGtyE+M0d8iBNiBzSSg2QGbkw2gSEMm3Hljkii/dQCvh1pK0ygl9HMmP0pUfsAzh0rA5lwKEj2WjEbd5Y3dOAUU+lQGbWs3bMs+qvxnrW4Igs0krLhr018s4CWtgjygxcOJJto019GvsO+3V0bkxzyFnT5u9BZo7SxZd0kdbXWJixo8xgzY60dKMVPaLMYLGOtDyjvT1i/8B+I9kv2gRkiRzeq2nzUiAz2qgjmHHkLQyU3Z9CzIjmaZhntF+jhX3OjmVCZuTQaFOfRpmB/Uay3wjLc6TlOeJLuuk9yEyqXCAz2q8jbM2Rlm60sEeUBGzNU06sTeEOhu/jItlvxO2NqRRIQigJ+K2ItCBH2JMnhL7z9kbseavvUYLnFvx7PfijKwirg7w1gqlGWntjcUDlqw8luILir4/Y/ZFmR5SoVyI4bSSnjbAgT2WWvZy7DSzIkVwYregRpQtOG2kXxu7fo8iccLxEXRXBcKdSsBPxpkWEBTnSnlxRGlHpQ83pkFZKwYoL3YgsUGkLPEjRnhzBd6f3im5MLBPSJTOO4LSRdmGU3SPOCdiTI+3JEQw3kuFG2JOn9yBB3m6IsCdHMmO0qUdxRPM0rDhy04g7yJFsO8K6HHkrAm26jrHWDinFWjukRHtyhD15KqXIjNKFPTmS08bi8qs66gLfndIgM94zRgv7nJQZGG6kdTmC4UZy4YrsiEo7hcghrbj5gsyqNzBw4UiLLvKgZY7I4r1SCmTG7+Mibg9H2qHRlx5VR2KeNbgZiiMq9QmRQ1p5DzKrXsdwCyOm2tvIGhyRxXulFOxZ5MJoYY8oM/imiLQgo+wese+4kxFp8YywPEdy7wjL8/QeZMavASMsz5G8HP+idkdkkYaWwQ4dyagj7gtHfhuI9vaIfQdnj/xWr6I0otJOIXJIK+9BZrRAoi9ApQbIjBa6iLsc03uYZ2T+aGGfkzsf2H0kn0fZPeLaBNeP5N4R9zwibZURzH96DzLjXeKIu8SRlr0Irh/J0tHCHlESuCE85cRqJPOP+Mou0u4Wwe6nUookKDPcEI60pkXcAp4Q+s57vzgP9Psn+45v5xLv9mKH7xEd2XVlZ/djmkPOmjZ/D17yeCc4gaUnsm3U1KPMnBbvBaKyl0fmdE/eE7xXJIE2XSdTax9mSDK1do/3wpg2r6E4PUxsWUBOusTDXZXE+ygJt4CntITaE2uHzMiaE6zuifb5BCaeyMQrkhGVdgqRQ1pxJgiZkaWjL0ClTLhYpDU74Rbw9B78UJJtJ1jWE+3lCUw8kbOj7OtEZoyygSyRw3s1bV4KZMYbwgk3hBNvCKNN18naEc3TIDNa1tHC60TunWAFT+T6aNN1IvtFm4BqmkPOmjZ/r3hjpHTh/SKRbaNN14k3ERK8X0xpkBn5bgIvT7wxkXAfJdHujTZdJ7JftAnIEjm8V9PmpUBmljKzkBnPCGjTdap+I2HNntIgM95VQQuvE23UCRbrRK6PNl2n6ksSTDzRtp1gsU60WCfcMpneg8zoqWJADqjkxNokp024SZJ4PwTtvU68D53A0qf3IDN6uEjOs2VuhtKISjtrToe0UgpkVt1YgrOn6scS9usk1ddmfPIeZEZrNlp/nWiVTrBRp+onU4oLU84z2KgT74ck3A9J1dUmOPv0HmRGG3UCZ0/VdyZuXCfaxFNxF8sb0AkMfsoJKdEqncDSE1l6wq2PqZQiCcoMtz4S7d4JlucJoe+0SoPJjx4z8S+9NP75+ur28eanqx+uPnz+dvPl4fZucIH8+f2Hm8/930z3L9P9x0/vH3/69vk//kf/v8fbj98/fr75zz7PP24evsJLsg82S86+P1o5ifbnn/8/b8tlig==

also explain, oops! I actually don't need this, overcomplicating things
then show
1x10 * 10x10
0eNrtXe9u4zgOf5VFPt0tPAvrvzTA3kPs18EiSFvPNNg26brpzPYWfYB7j3uye5ITKTpx2ygTs007ioMCjWjZosgfRUq0bP89Obu6a27a+WI1+fj3ZH6+XNxOPn76e3I7/7KYXcGxxey6mXycQM1qtlh9OF9en80Xs9WynTxUk/niovlr8lE8VFuumbXz1eV1s5qfb79KPvxeTZrFar6aN4ktEvfTxd31WdPGZqtd7KvJzfI2XrtcAM/YnnW/mGpyH69T+hcT+cSrVu3yanrWXM6+zuMl8bzb5hwuuX1cjrw7UarJ5/nVqmmfHl3d30BPvs7b1V0Uc921JPaHtrmIx/6MVVGCeHixbK/xtNjjm1mLPf44+RUP3IG6xcPv8e8BNPdEbMkW27y52F/aplkME9xnBVcDBQ8l4a2yYuuBYvuSxJZZsQ0b7SLM3GYFt2y8ixDcZQV3wwR3oiRDN1mx/UCx65LE1lmxAxvtIsw8L7io2YAXIXne0sXAGZtTJZl63rGJgVM2J0uSOx/JhGLjXYSl5ycvQrMRL0Ly/GxVDJy3OXMcqzJh2XIXgfgOyYfO23RJiOeXo8Kz5S4d8aFzN3skmZeaLXfhiEt+rs2+ueSQtHw1wfnZNvfmgp/fz14t2Sb52bYSEM9PYCQ/31aC4Pk5q+Rn3Eow9fwyRfIzbiUInl+XSn7GrQRTzyciJD/nVoLg+dyT5GfdSjD1vOCKn3QrQfC8qSt+zq0EU887N8VPupUgeD6cKX7WrQRTz09gFD/pVoLg+Smr4ufcyl6dKX7SrQTEdwjOz7mVgPiOPSD8pFvhiPNzbmWPcc1PupWNuN7M3Nrl2fJm2a6eSxtUJ2uUtG3+vGtuV9N11zPCAcMt/DYTptu7s6hoZPN89dtpN2xtRLHzZf7N0bqZL/54NbQ0W/Dw5oLfN1dXy2+v5ZM1P3FUAuY7dubxE0clCJ6faWvHRrwMY8+vrrRnY16G6PkVteYnj0ow93wOxdRswcvAPJ83M4KdNysB8x2CS7bgZWC+w9z5CaQSMM87OKPZgpeB+Y7d9oadOysB83w8N5YteBmY56evxrGzZ2Wv1YxnC14G5jtED+z8WQmY5xeptmYLXjrmVrAzaGWPcyvZghePudormefdrmSe1Xs1Au4UGtFiayNDs0NrZ6sFgnAxb5Oa8VGpt4TkNw4a1WR+O4XOfp5d3TZbNWK5qUJdv7lZfrucr14tl28dW3LxHhto718t+nhuwqwMyPOTTBvYkpcAeX5h4WpuorAMyPNrSSfYkpcA+Y4HmCU3T1gG5PmUkVNsyUuAPJ8mdJqbJiwD8h2SG7bkJUC+w9YtN0tYBuQ7/Jvj5srKkHxHMPdszEsw9h2xPLAhL0Hw/LzV19wcYemLNC/YkpcA+Q7BJTdFWAbk+eWpV2zJC4dcczOExY9yw5a8cMjtfplR0eG8tZHNTGj7awyzmdbnSU29XZebdqex+mK+VuzneXu7mm5ep/gd3TWz80t4q2LEIzYz7cBGtS9vmjbJ/3Hyc7xyebe6uRvc9nY1+8EaCiPTUNjLEENYG2J/BFw1X5rFxay9n2x7t9Zm8rJqZ4tb2Dv84ay52rKB2GzybXHOuvVFXYLTmHwG4ram5d5NW/Gon4+aFnJb22r/tutdbW83vvN5e343X03bZnYxvZwlu1nFPkQLXLV3TbU+ozueTr1eXsQubXUqQXO08UzRflvThqMMuedAPIQuNl76ojmfXzTtd24aDewyNfrEcfSpT2w/8igm/WsCr7FNbuPpy3P38x2Z1+c5noLUaBTk2fea5Ds8MDM7f7Xb3iGwJVdvLvnFcvVqryWqa/a9psIhFzX/nkvxoks26oWbu2JjXrjgmn23qXhjN2zRC8fcsm83FY+5Y4teOOb8uy7FYx7YopeN+eC3Y8ujwXzw67HlsWAu2XecisdcsUUvHHPNvuVUPOaGLXrhmFv2PafiMXds0QvHfOAczg9PPxe2/V/0Xp+9762xXsDb64mI17o1Vh/qvlhsqc3cFxO912zvk9pe31k9aO6/6/5quWhSDrunjWcm0b96umhW35btH8gF3kZO90TSC7p7djIQm/ni8/JxT8KTnvzvP//9bl+Q/boz0LN1gr6ZUg9miwt+kj4hHY/uwTn7/RTBvt2uxnEzWfReVL7XoAk/wA2z357dDPr1pXaWtSDF3o4wGgsaOCM3m9tG+p0jNbrC15qx9N6Dvs9IMmGgEg4eft4tlmyJa68bS7puviiWDNxZIN4C3rd0lEmJWfUMfURTPfECP/a4r3eM+6EbBuQ7Ss74qk21bl4e5mNoGwbqIF/s2LSvD/Lu+E375iCvF9u0bw/00roNB3eYJ4M2DPxBnp/etB8OkaAJPQZwo+HV8yC73Etvu2dzFV3B8juBh97sqs2egac/N0wcJhUVptezv9ZBEuUfOjXY/nnHmrcHzRzdHjRo7+Z+imYw/dwur6fzRWyrmwXlPo85eFnb26pl3jQR9GRRMvg6/sLlcnbTfLhctvN/R/FizQNrFvqo33tlQTKQycGQhRNk7wvZ4KV/b6PUCbJ3gUwPhay3z+kE2btAZgZDVp8ge1/I7GDI1Amy94Vs8HOHvU1CJ8jeBbLBD0L29vicIHsXyAbfoO9t0TlB9h6Q9b4StC9k9gTZ+0ImXrANRh//Nhgtedtg9GkbzJFug9GKvQ3GjGQTg9bsfR6jUZHh7RTS49gpNPijXps18Vt+bxBj+demjWaIx19n74sevL6El1n3hH+L4fNY9EEzqS0zoJcOtTo7zvzwvPPIdSmyuhy+IqtHrkuZ06UZvlSSI9elyupSsB/lsUf6dIORw5MnIzcvnTUvNTyrMXJdmqwuh99THHs4tlldDr7Z58cejl1Wl4Pvwvmxh2Of1aV7QUrRHn9K0Qx/KefYY3PI6jLw0rP2lJ490vSsrdnpWTeS3GPvU4SDco92HLlHK9nZ69FYkHpBiPfHH+J732wcFJb8KSwda1gy7LAUxuJULNvvjkZFjhe5/Ugit+eHJVOPICzxVkumPoWlIw1LrmY5lMNaxI/jUNwLdscZdfwOxUnurMbIkYTs3kdZB/lcdfK5x+pz2bvjxjNoeLvjjBpJWLIvCEtmBGHJ8XyuOfncY/W5nj1R0WPxuYHnc804fK6v2VF7LBbkX7Jacscfljx/tWTHYkLM1ZI7Re4jjdyev1oazaBhrpbcSCL3ft+aNp0vCdtbcXu14sy6lb0/FCz8S+5bhBEEzsAOnH4kPiDwXtdvwilwHmngDIIdOEczaHiv6z/soPlxAmd4wS4vK44/LAXNDUu2HssIM6ywZMUpLB1rWGLv8hrPoOHt8jrsoPmBwpLfayXm6dXdVm1vJezVSgjrVvZez8l6Mxlvl2fLm2W72tIyPUBmIfPZNn/eNVHf64eIM48Zg06iVr9FjKHik6hEJSvxe/VJQklgUcWiwZKOJYslA9UKixaKGosuFgOWfCyJGosB6h0W4UglfSoDL5GaEMBNpDbgUKUSZzhUqdQhASxF4g4/lUp9EsBUUJvAVhEv5Ju6AD+VSj2TKCMJCXx16gNIU8nUJohTycQLDlWajgNfTceBr6Q2kS/xAr46HYdDlSEtAl+VeIFIlUryKlQvHQe+JvEC8SqVeMFPZZJcIF6lkrzwUxnihXxTH+CnsomvBl7ebsrRY6pUlnBcduXoJnQqGzhuoAx906mfGsGndlAnqT8adZL6A4cqS2Xom6P+QN9MKsNP5ZL+QTWVoTL0zSVeBnVCZeDryOqAr6Ey8HWpD6CayiS+8FN54gV8bSrDT+UTL1BNZamM+km8rNrInsohldH2yCASQaiCQiqbemHR/FMvQAmVTcjATxwMqRsOxU8XOxwCNREof7ID+IkVNKhQAckoHPKuU0ccaiDxA0VULvFzafBRBTKnoehRB4mfR+YiKcGjEhJzj8xpNIJiKp+Ye2ROQxAsqvKuK0sogyl5HI7kOeAYElQTW6YRGQmNBNZgh2kMJ4J8SyTgGupkADcUEiQBe0njNZhk11hOPC0aM6BRhaSWgJroPAvAEZVEvqVOSJA3qtEddX6nRk6qq9N4JvmeGlVCIxlxqeDL7olCTXReqk6gBKJSX8iboVuEL0UnKjlGaiW5xs5PitSXzoNiXwRxSA6SvBzCVMEXShOFfSHvgJpeWzB8uTLy0AkkouIg0kRtYELsEA1F1AYbRLwSWq0piZQkKh7XmzM1UqlOIlwy8UMnLMjjAAXXkXzRKUtEPF3XDUlFlFoPUPjdmAD+VvCljnRdMi/SkkT5FMkXfzVaSKJQBqXWFPSF9Knko7pEmTUFZxIHlWQgxJR+dGai3JqKZ5I3hHOAIsSUfXRmosKagjO76ImjjOIJWEr/TKR0vabgTNJZPAco0rVGbMmjom1U8By2JKqHn06h2yQctOwjhuFDkP9Fa0BKEgUcwrpOI5Xq0K7JPwMVz7TdjMCgDCZhq1ETuusZDv2o647SSKUzk+wdB491geqSzXc9Q5uIFNbBUURFEqWRSnWIuyErgKNIpTqUNqIiidJIpTrE3ZAVwFGkUh3KZyzVGawjSzaWxqYkSm9GqkHZbdcX19cnhkHQoCKqp08Mi/A4UUdJpCRRcKZe12mkUh3aRPyP3DGICtvNztAKKCpinyp4lkIS1W8lIe1Sz6x+dB2OcJopYJ+QkkTBmWFdp5FKdej5XNdrHB00D4G2JXJIvUabcDTerX/UCuosXqeI6rXiUEuOLMShJhwh5nB0OMIBg7qgGI29R6qrU3hmV9e/DkeOo1HlcKy4br6LOvP1murXJS2RLTm0F0/yObQXR2MFJwzQF9WjwppK/dREKaxLHNB/0jwKZUEqtRmoZ4ooiddhKzj1EDTPwj5VcJ9KEhWPe5Id5yJwj0YQJZHq6hSe2dX1r0OdedKZR53RzAX5VpDC7qh+HerMk85g9lfB3TmDlMMphycKpQ0dP7SXQF7Do+yhkw9lD3pdp/DMrq53XUC9BIqpAUdcIO0GjKk0rwGqX4d6CeSJAo6qQOM2oHyB5Av6UR2OqkAjLuA4Ct2KyT6i0ApoVYA6oMlXXDDOV811XI3CB99u2vkClqNXs7MmLsYn4i9R//TzT6KG3+vZ6vru6qd/xH+r+fn9+VXzz3jq17gkxYWrsTLoEIxTRmknHx7+D3lt6oo=

based on this, then go into the new arch
new network archiecture, now that matmuls are actually easier than i thought
1x25 * 25x20 matmul
0eNrtXeluGzkSfpVAv3YHyqLJIvsIsAvsfd83BoEh251EWFvyyHIm2YEfYN9jn2yfZFlFdkux5Egqpd0T9YcBMlXdZJFVPPrr+qj2N6Pzq7v6ZjGdLUcvvhlNL+az29GLL78Z3U5fzyZXfG02ua5HL0aTxXT55rpeTi+eX8yvz6ezyXK+GN2PR9PZZf1u9MLcj7fUuqwvppf1YnsVe/9yPKpny+lyWsdWRXl/Nru7Pq8Xweb4I3bGo5v5bag6n3F7wZzPx6P3war33/Ohkcvpor6It914FBxbLuZXZ+f1m8nbaage6iSjZ+HepRi65avrWujSq+nidnm24djtcj6r2ReO2HLC4TOsXN9MFtK9F6Pvhy6u1z6b1cuv54t/SSuL+nL0Yrm4q8ej14u6Dp18Nbm6re85ig+bXL6/4SbfThfLu3ClDUos8Xw6ezX/sCfWPejK//7z352dkfbb3nDX7hsr9VnqwmR2OeJBm98tb+6WD2fKjn6Gzsno79Py/ct7CcWDCWHHH5+Oj88Jt+ecWNl9MC0OHJR6cvGGnb2t2czZB7NkflOHgZFejL4YNdE81PbWANFhK6Z8ihWzw5s/je43Fs6Rc+yR2eMOnj3lsGaPb8su5ufzm/liuRkTqlJM8tC/Rf3VXR0cezW9WtYL8fQ2hiiOW/tseLmtuVy3vRfY3k90ey/U23s+jAVa6rb3YhDbe6Xe3gcye0y2Knx3HpqUZh7f4avQxa9CG8FGqHJVv65nl5PF+9E200qoXmEvP9G93OixejmQ5agE69UgdnOjR+tDmT9+r+08d4rtfAXNG28+GnoX5mRsJc8eBr/cHvzVe8Ij7wy8Caa3ig+u7pyh617O5otrKbSx3V/M72SIwvR7ySmp27P5Bzv7w4gUBy1Wl56huelxsTbz8gPff6Bfr2kuPrJeSxUC6DZAQAB9IoBKiwA2N5HT3MFtpkIAvW4qT4cArNEigMHMH3vgY9q0j2m7Z4S6ekz/8NDH9Lg1bnca/5HeOO00/mO9cbfT+E/0xv1O4z/VG893Gv+Z3nix0/jP9cbLncZ/oTde7TT+S71xTtfssP6rI6zvXqO/PsL67kX6myOs716lvz3C+u5l+rsjrO9ep78/wvruhfqHI6zvXql/PMJ6+elf7tas716rfz7imbR7rf7lCOu71+pfj7C+e63+7Qjru9fq34+wvnut/uMI67vX6j816YatWI4OxHL2c8VytkssZ7vEcrZLLGe7xHK2Syxnu8RytkssZ7vEcrZTLGc7xXK2UyxnO8VytlMsZzvFcrZTLGc7xXK2UyxnO8VytlMsZzvFcrZTLGc7xXK2UyxnO8Vy9nEs53RkkR0KWWS9LkB0cgFiezfvz2RKnb1azK/PprNgq2GYHgnfgfSspwfvCng7wNsB3g7wdoC3A7wd4O0Abwd4O3jKt4PDf+bgDsS/HZ1rOLie/uzDm8lN/fxtvQguhOv3isNZD3q91xmq7eNVqs8x2YGcQ6l0Z/8IZ/9O9OwfKU+20SBOtpH+ZNtAdhRanWxbLiazW/4t6vPz+mrLD1LdKrmx+TPmbaZpf9PuI6a3x/1iuri4my7PFvXk8uzNJIZsGbpw2+wiTYnmeix6Pb8MPcq2xsLt32H/eIfLbab9gYmk7OCA4AAhDhDiACEOEOIAIQ4Q4gAhDhDiAGFHBwgpV2M5BywHLAcsBywHLAcsBywHLAcs1zOWO5witAfm5U6EInwzX0z/HdzrmySkUj1iDiPWy4hVahr+6dbYBg2+/6BtCfaxhE0itbZ+WzVTR9MhmhvR1H1OL8eXr0+VUHfqz+nlA/l4sdN9Ti8fyLev1Z/TG8z88eqP6RQ9509lH/xErx4u15y84C/objN24Ffz6MCAdv4c6++htBX6fsqHUtPPYx5KpeZkysbXlo3dZrvSHNPZYvvJzun4w868Of8Uk/0pH0BxRj0yV7w5cHvNH2yvQyWkOv3NGnVJSLkuCSnfJSGVd0lIFV0SUmWXhFTVLSGVdctIdUxJdfuzNUPdklKuW1bKd0tL5d3yUkW3xFTZLTNVdfvrtazbn691S07Zjn/ARt3+gs11+xM2/+hborfqw0YFDhvhsBEOG+GwEQ4b4bARDhvhsBEOG/V72MiTGsvlwHLAcsBywHLAcsBywHLAcsByPWM5pz6GXOAYch/HkL1Xj1iOEetlxHL1UeccR503oqn/Gl6BaG5EU/lXWAscHD/Rg+Ne/1dY82Ec/M2V36orBnFwPNd/q24o82fFhd/WV8HX+Y6Dn0WKz75/p36977GF0TgJZ9eTd+1uIO8bh26CWz3SZ4QrZISREUZGGBlhZISREUZGGBlhZIT7zQjnTo3lSmA5YDlgOWA5YDlgOWA5YDlguZ6xnJ4rrsAV98EV57l6xEqMWC8jpuejK/DRG9Es1dEsEc2NaCr/zloFdv9E2f0iU7P75TDY2cLo2P1qEOx+YdXs/lDmj5oLLwzyp8ifIn+K/Cnyp8ifIn+K/Cnyp/3mTws1F15kwHLAcsBywHLAcsBywHLAcsByPWM5NRe+d14OzOonZVYLNRe+N/rGiH3aEVNz4U+4xj4b9rZQc+FPOP8/n2jquPC9Jya48M+NCy/VXHjfz5en4jJLHRfe7Zr51nDhpZoLH8z80XPhhPwp8qfInyJ/ivwp8qfInyJ/ivxpv/nTUs+FW2A5YDlgOWA5YDlgOWA5YDlguZ6xnJ4LJzCrfTCrpZ4LtxixXkZMz4UT2NuNaOq5cItobkRTyYUTuPAT5cIrPRduh8FlVkounAbBhVd6Lnwo80fPhXvkT5E/Rf4U+VPkT5E/Rf4U+VPkT/vNn1Z6LtwBywHLAcsBywHLAcsBywHLAcv1jOX0XLgHs9oHs1rpuXCHEetlxPRcuAd7uxFNPRfuEM2NaCq5cA8u/ES5cJPpyXA3DDLTZEo23A+CDTeZng4fzAzS8+EFcqjIoSKHihwqcqjIoSKHihwqcqj95lBNpifEc4A5gDmAOYA5gDmAOYA5gDmAub7BnJ4RL8Cv9sGvmkxPiecYsn6GTM+J52BxN8OpJ8ULhHMznEpWvAArfqqsuNGz4vlAOE2jZMWLYbDiRs+KD2YG6VnxColUJFKRSEUiFYlUJFKRSEUiFYnUnhOpRs+KlwBzAHMAcwBzAHMAcwBzAHMAc32DOT0rXoJi7YViNXpWvMKQ9TNkela8Ao27GU49K14inJvhVLLiFVjxU2XFrZ4VLwfCaVolK14NgxW3elZ8MDNIzYqXBolUJFKRSEUiFYlUJFKRSEUiFYnUnhOpVs2KlxnAHMAcwBzAHMAcwBzAHMAcwFzfYE7Niu+dmQPF+mkpVqtmxffG3xiyTzxkalb8CVfZ50PjWjUr/oQr4DMKp44V33tqghX/7FhxUrPifT9jnozTJB0r3u2q+faw4qRmxYczg/SsOCGRikQqEqlIpCKRikQqEqlIpCKR2nMilfSsuAWYA5gDmAOYA5gDmAOYA5gDmOsbzOlZcQLF2gvFSnpW3GLI+hkyPStOoHE3w6lnxS3CuRlOJStOYMVPlRV3elbcDoTTdEpWnIbBijs9Kz6YGbRixW/vzkOb0s5GXHh7lri4+3XUf1W/rmeXk8X70VbbTrene+zpJ7une/We7oayInPdnu4HsqcX6j19MDOo3GtPz51mT1fidPylo5Pd070epw/l79R4JU4fyF868nqcPpgZRLp9F9/SO91916n33aF8Cc173b47kG/p+Vy97w5mBhWqfbfCr7VOd98ttftuNZTf2vhKte9WA/m1Vp5p993BzKDc6PZd8IEnu+/mVr3vDoXNyUm37w6ED8ydet89yRkUovx18Ihj/KUZm7Ed08uxSJQkG/5zSXJZEsPNsQmSDQWLVjKF1OEaxdgmKexGXCeUHzu5TdyIXHPhWiW1WTK5iLmYpCSVSWKLLklUJZHCba5ScG2bRMsiN16KdRLJhpJcp+KSTkqabOzHxo99KzuKionmqJWpkcW2a+SwtySZuIwYlTBUjWxZ5r7wbW6Yomy5vNRlx62J5b10ooydYOd9Fm+wf5QaKGMD1Mg2a2RpzDWyLxqZuIzUZe9t2ciWZRmlLHaComy5PNe1Mg1i58IoWu6PXPdBzm0jhztptFmmZJP7b9PUCF3hqSPXuc8ujhU3z3K6HvpZNdcdy3Kd+0zRR740zuNABpn4Opfn/3E/KcqWr8uU4/67ONrkuUzsD3HfKMaBeMKkPovsfSMTTzQpw31zqa0qLgPbyGESsOxM9ItamRpZfHSNnBeNTFxGJj9PGl81smVZbFLsP0XZcnmpy5Mmj+PieCxcjL/jeeKSnSLOH4oyNXPJZ6tx5P/xOHJdz33O47h46U+Mm+c+hJiI7FbxETnPG5l4vkkZz3JcyRwavi5lijh2IpfRX2rkPGtk8d01clE2MnEZscnzoWhlyzLb5NscE4qy5fKySbBfRfQrZ1/y6EsuMUw7jl/5InLRysTjJWV4t8njnMnXfBG5SHLqG7WyaWTpp2vlopGJy8i+xf0vs0a2LLPNIvWfomy5PNdll8Zl2vPYryL6VbBfRfSrWPNF5LKVifsgZdivIm2ja76IXCa5in2jVjaNLP10rVw2MnEZtskujauskS3Lsjmb2H+KsuXyXJddGlfRr5L9KqNfJftVRr/KNV9Erlo5tBv9KuXpEP0q13wRuWplNy7jWiur2E9qZdPI0mcXZeLrbJNdGpssaxQrClviAuwBRdlyDXn0yKMhi65V7FoVXavkMRhdq9bcEdlkrRLajr5V7FsVfavW/BHZZEWjBLtZ9K7iHbVKcpV6TivFNEp0w0WF5E58Voq7Jms1K5o82jKTHKOkWaknT59MnE7PZpPJUzDzSZOHfpYnbd3bpBnfatyX9OTKctGKpEWny1RSvG4eupk8FE3ZauGebe5VySNa00yrRf9c0kjuSXtGItE8UY1EwqZIRLTQQgeJhEmRiMjApkhEPJAQjxEUwN5GLfqeImHEd5N856tj/iCdTRrfS5Ewxbq3UbMrLbQRHhxRk0hQioTAAtPgiKSZVov+uaSR3IvwRiKRnsESA9HEpjXJW0qalXpixUokKEXCSiRs8t1KJGyKiwCN1tuo0UrjviTfrUSiwTb2A9+jRisttBEea1GTSLgUCQEbJqGNRjOtFv1zSSO5J+0JADEJIUgMRIvAzyRvKWlW6okVkkgkNMRfp+GSKRIkkaAUCfrAdxLfE5rhqyT+Re0Db0m8DQ/BqIm36YnM4x97TWuaabXog0sayT1pwUVvfatZ0cSmQB+TcJARwMP/RqgbvU29ZrC9QrsCadgKrWl5q8UWXNJI7kUrDOtMg5MFDLEW+5Kn9ihpVupFK/LK4FPkXZWs0JpmWi3adEkjuRcBu0QiISVpVzRpXQAVt0BJs1JPrAjAMgklGYFYXI/WNN9q0aZLGsm9WE+i5MtWs6LF1n1qgZJmpV60InFJeIpnQ7RCa1rVatGmSxrJvVhPXkQSYpR2RYutV6kFSpqVemJFgBq/hks9gWdcj9Y0arVo0yWN5F6sR8kKJc3KPfcyvM9Ol/V1eNM9v7qrbxbT8MI8Hl1NzuvwWjwy76x/9sUz69/Z7Nn1ZHl9d/XsO+Gf8K7+/uKq/m4o+rZe3Mp7tc9t5arKF+TJFfb+/v/ZTD2G
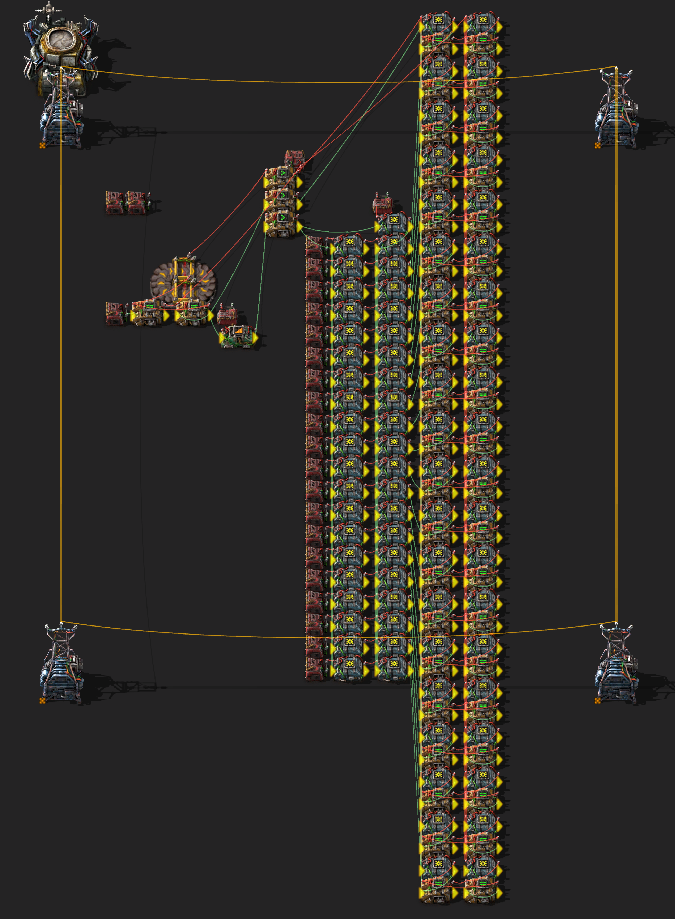
1x20 * 20x15 matmul
0eNrtXeuO27oRfpVAv9oD5UC8kwu0QO+X0/u9CALDu6skRr32HtnOyTbYB+h79Mn6JOWQlO2svZE9DleJNX+SIUUNZ4YXfZqP8r4vLqer+raZzJbFxfticjWfLYqLF++LxeT1bDyFutn4pi4uinEzWb65qZeTq+dX85vLyWy8nDfFfVlMZtf1u+KC3Zd77rqurybXdbP/Fn7/sizq2XKynNSx11C4G81WN5d143WWrZ5mfjm/nTfLoixu5wt/w3wGvXglRpfFndelrFfc1N+u6sVy9GoyXdbNApos6itoHfWvbX15D+Y+6I6XH3d2p28n2r6/Vr7360kTOysuZFn4UC6b+XR0Wb8Zv5342/09G70jf/l6kix7X7yaNN7sTfiWd7dgx9tJs1z5mrVhscXzenz1BgLpnfNqQNdiOYYh9BGb39bNOFpRfOXvnK+Wt6ujdd/vC5AoPzKuj0fHHRidpPRBaLZLL3Yj1Rq/nM9qCMkHsfDm3Y6bYN5F8QNv4vbdo1m9/G7e/Cv00tTXxcWyWdVl8bqpa2/kq/F0UYcoHDk4k9mr+QNL3ANT/vef/3YaE/pfWwOm3bda6lEyYTy7LmARxTF+uHI77PTGhdV4SM+wYPZMCHn0ilHDWjHquBWjnmLFdHjzp+J+Z+GcOMcemT1603p16VsGVx/d4LV/whTf+k68Cn/LtH5dz67HzV2xR7PB7uS6Gsa8tKidXDPayc90J3fYnXwoK4ZVqK0875L5bLZyxg7ay1nFjt/M2QaXt4P90dBb/XUbfP4w+HZ/8DcvCY+8MMAST68UH9R2DsC2l7N5cxMa7WxmV/NVmME+ui/h/Wgxmn+wbz2MyHFA3LZPUNHjXGyX7Qe+/xA/HdNSfWQ6SjQA4APZzhQOAQhCAGeKAJhGQ4ChrBmDgwBiGBDAHveYNm79mJYHBijXY/pHxz2mOXjf5jA7lf8Yr1x0Kv8JXrnsVP5TvHLVqfxneOW6U/nP8cpNp/Jf4JXbTuW/xCt3ncp/hVcOrz8d2n99gvbuNfrNCdq7F+lvTtDevUp/e4L27mX6uxO0d6/T35+gvXuh/uEE7d0r9Y8naLef+uXuA+3da/XPJzyTutfqX07Q3r1W/3qC9u61+rcTtHev1b+foL17rf7jBO3da/Wfx2p/+RiWc0diOfulYjmWE8uxnFiO5cRyLCeWYzmxHMuJ5VhOLMdyYjmWFcuxrFiOZcVyLCuWY1mxHMuK5VhWLMeyYjmWFcuxrFiOZcVyLCuWY1mxHMuK5VhWLMeyYjn2KJbjFY4sUmdHFoG+27tRiNjoVTO/GU1mXldLDzwSPoYLnxwK18aPpGdd9eBdgTK9lOmlTC9leinTS5leyvRSppcyvU+Y6eXi6FMf7MgXhEynPo6+D38y5M34tn7+tm68C77+HnH06IHVB50Q2j9e+JNtchindDjyZJuik21nerKN40+2DWXNIE+2qUGcbOObk23LZjxbwIeozy/r6Z6vUS1bJzfMgbG5mjRXq8ly1NTj69GbcRz1pTdh0S71tkVbH5vezK+9RdVeg93hBlcfMXjfJ6DV4ar546rtPtXsyHP+5uhYE+lMpDORzkQ6E+lMpDORzkQ6E+mciXQWHI3lNGE5wnKE5QjLEZYjLEdYjrAcYbmesdzRFKF1R+blzoQifDNvJv/27vVNEgqJHjFNI9bLiCk0Df90a2yHBj980PYE+1Q6K1E2e6Op0dHUFM2daOJ/TU8P5HdRkT+nZ+jIwZkeORD439MbyJqRyN/TM4M4ciAZ+gNs13P+NKzyT/TqITnmIAP8tvA+ZQJzjGPnh4ohgfRE5zikPO7bo+rIKZD9udLfQ2IvWP+UD4nWzlN+PVthztLsmZD7dOsjCRjxYAMZKuWS9asskZNykTkpF5WTctE5KReTk3KxOSkXl5dyqfJyLplJl7wfZjGRl3aReXkXlZd40XmZF5OXerF5uReX9/usKu8HWnnpF575Ey2R9xstmfcjLfX4e9Bx5/Mtf4oXgad8WY5o+7HoWPRhI0eHjeiwER02osNGdNiIDhvRYSM6bESHjfo9bCQdGstZwnKE5QjLEZYjLEdYjrAcYTnCcv1iOVWhjyE7OobcxzFkxdAjZmnEehkxjj7q7Oio80408b+GZymaO9HE/1adHcYhWIX8rTpHB8fP9OC40rhj0W4Qx6KVQR+rH8qOsuHCF/XU+zrvOCogY3xMdWB8tm2PPRRlEkY343fruR7eN45d4ns9QmeEDaOMMGWEKSNMGWHKCFNGmDLClBGmjHC/GWFdobFcRViOsBxhOcJyhOUIyxGWIyxHWK5nLIfmig/OyxFX/Em5Ys3RI1bRiPUyYmg++glH7Ivho7VER5NRNHeiieOuDw4lcddfGnetNfa8R9/Pl6diZzXu76zlXTOfDbuvLZbdH8z8wXPhgvKnlD+l/CnlTyl/SvlTyp9S/pTyp/3mTw2eC+eE5QjLEZYjLEdYjrAcYTnCcoTlesZyeC5cELPaB7Nq8Fw4pxHrZcTwXLgg9nYnmngunFM0d6Kp0MwnHwZzZTTutICg0wJnelrAoL/lHsyasbjTAmIQpwUMnguXlD+l/CnlTyl/SvlTyp9S/pTyp5Q/7Td/avFcuCIsR1iOsBxhOcJyhOUIyxGWIyzXM5bDc+GKmNU+mFWL58IljVgvI4bnwhWxtzvRxHPhkqK5E008Fy6HwetZJBeuiAs/Uy7c4rnwoawZJBeuBsGFWzwXbih/SvlTyp9S/pTyp5Q/pfwp5U8pf9pv/tThuXBNWI6wHGE5wnKE5QjLEZYjLEdYrmcsh+fCDTGrfTCrDs+FaxqxXkYMz4UbYm93oonnwjVFcyeaeC5cD4PXc0gu3BAXfqZcuMNz4UNZM0gu3AyCC3d4LtxR/pTyp5Q/pfwp5U8pf0r5U8qfUv603/wpq/BkuCUwR2COwByBOQJzBOYIzBGYIzDXN5jDs+GOuNU+uFVW4elwS0PWz5Dh+XBHDO5uOPGEuKVw7oYTz4jbYbB7rEJS4o4o8TOlxFmF58QHs2qQpLgbBCnOKjQrbitKpFIilRKplEilRColUimRSolUSqT2nEhlFTYrdzCYo6zcp83KMYZNIz3hkH05aSTGsWmkvlfAk70QM4FKI1lGaaRzTSMxiU0jDWfVKFQaKe+q+XzSSEyj910+lBlkcPsu/aXT8913LXrfHcyqcbh9dxh/65TxCr3vDuQHghlnuH2XflX7bPddztH77mBWjcDtu2og++7mjWmxuvRtg7M7YYG/bh/Cou+3c3zT+nU9ux43d8Ve3Qq3YdFPH5zvhoV/vdJD2bDQR2GGEyLcURhrBrKnu4P29HBc/eOburfvOx8tsO4FL1lpSvayDBITpQgi95U8SR6hyiD6i6ml9BJc9uVShVt8uRQ6NIRmKjSU/rJbS4wnsb2s/D0q3KKhxqtqRf/8AtnAXTK09eaAyIMoSpsqpZegzkLLKlhiwZKo1oLBVWjqoIFO4rrW/8dBhsbQfwlRhp7B1lLGwDDwkscewZqSy1bmIPMo+1aqrZcgh3oF/ZpgGAv+itiZgvZJvwadupU39cFnE4MPhirbyr7TOABBFtEGP04cbA5twH6ehktAGx3bgP0iDTjYL0xb7xWqtl6CHOrBfh7t58F+HvWD/TzpAfuFa+VNPdjPoz2CQZtojwDbRIyhCPMm2h9kxVpZwCiGNmCbiPERKs4z3soqTUSYKirphH6VbOv9vbatlyCHepgwMk4YqCp1HBcBU0bGyQEulcq08rpewljIOGlkiHnsS8I8kdEG+A/GQkRZtHNJQqxUtEeazXjBf1Af9IBtKvUVbGBxuVSb+ARZ81YWMC6hDQM5xlnxTXyCrJMMtukYTwgTyKne36vaeglyqIc5oHTwBapKLYPNCuaASnp0jJWIMof60AbGRUd/Ffiioy+6AjnarNnGlyCbtSygr9AGdh8d/QI3oD60AftNklX0S6xl08rBR9nKRraygDZBJ9hvVCtzkIPOZL+IMof24V4YI5PuBb9M9MuAXyb6ZbZ8CbJdy6I00RcDfpm0xYmNL0G2a1mWJo4RmFjaaCeYCHKqF9Am1W/aB7+i/QbWpkk7J/hlTStv6mEtmLjPGPDLRl8s+GWjj3bLlyC7tew35uiXBb9s9Mtu+RJkt5Zl6aKdFuabTTL46KKP4B7IqV5Am1S/aQ8+2uijBR9t9AXcK51p5U09+GijjxZ8dNEvBz666K/b8ivI8ElRKojSRScdOOmik27LsSDDFxip4FuwuPRceDRU0W4Xng1VdBR8DIV0RUBk0oV1lKCqdNFTB5666JELD8rKtIXNBXDVRVddeARWLD34qlDiqbTtYirBszGV4HkpUkseSukJWG17mkqMrUu+FW9LwXNmUim4ztreg++Mr6+JEKP22iZiobaEM9MilUQoxZYhCEyuS9vXbLAzBgIOFbPgX7gGsCFYHUssWJ2e3gEGsIQbgoWh1F4TYWDba5thDrUlkHIilUQoxZYBCzG7Lm1fi5FQCZAEb3lrJ2xLUOKpJEI822tb0WUxEi71HiLBXGoZkBLn69L2NRd6d7F3HmZIi0sCAIESTyURxra9tjXSUFtCgkakkgil2DLEM+EDKG1fC7OHJ3wECHALjalki9gq2XUpWiZTSYRrUaf5oBRmAYdZ4CHwZFnfeFx8OV3Vt83Ev9+UxXR8WXugXrB3vHr21TNevWPq2c14ebOaPvue/8e/Wt1dTevv+6Zv62YRQLfS3EnnlBFKSMPv7/8PkhzA+g==

1x15 * 15x10 matmul
0eNrtXetu47oRfpWFfrUH3AOLdwVogd7v9zsWgWHHykaob0eW92y68AP0PfpkfZJySEn2xsrKopZWN5o/yYShhjNDDvlxZmR/iObLfbrNs3UR3XyIsrvNehfdvPkQ7bK369kS2tazVRrdRLM8Kx5WaZHdvb7brObZelZs8uhAomy9SN9HN/GBNDy1SO+yRZo3P0IPtyRK10VWZKkb1f7xOF3vV/M0NzxJxSffzDfbTV5EJNpuduaBzRpGgXEnmkSPhpnQhnOefrNPd8X0PlsWab6DPrv0Drq7AWphbw8g75PxaD3ebj/fFTM7zPMjSqNz9M1+tjQ8zDPL9G26Xszyx6iBNbuMNWPdWXPy6Tk6H4XKchT2tTDjLLLc2cjyMkugyDfL6Tx9mL3LzPPmoSPjqfn3IisN+iG6z3Jj7eO0F49bEORdlhdG+OiotO3xOp3dPcACMHNi2AAvYwpYemamN9s0d2a5ib4yT272xXbfmfehaV5FdwvpcVlI1n2rET9tnzj5WpQW4k8tpJstdPTDZ3ySRLXXftTaotUfo1NPWW/yle1kxN/Ociv+TfQ927C3djSufwt70G4Kwt7Plru0ySKKfGIPazJIaQ5x4YIpuT5ZLad/vfFePB/p/v0Itlm3Vp7u7ZctmNvGJaP9tx0xDqdKui2h2jw85BKqpC8269StlRNjnDnN6dPTdVp8u8n/aUfJ00V0U+T7lERv8zT9yJM6zk62vt88kYQ/EeW///5PqzB2/FoaEK32hHRaijBbL/y9wQhn0cslIz/jM/HE/yQaidPEcUev0dfwmtYz6HDmPD3X2XMriHY9qeP6pJYXWijUSf2Dric1qZnTVuY/9GfOWpn/yJ85b2X+Y3/mopX5T/yZy1bmP/VnrlqZ/8yfuW5l/nN/5kkr81/4M4cDooX7L3twb/fRX/Xg3u6kv+7Bvd1Lf9ODe7ub/rYH93Y//V0P7u2O+vse3Ns99Q89uOvPf7874d7uq3/qcSa1++qfe3Bv99W/9ODe7qt/7cG93Vf/1oN7u6/+vQf3dl/9h0/EoRHMsa5gjn6pYI6GBHM0JJijIcEcDQnmaEgwR0OCORoSzNGQYI4GBXM0KJijQcEcDQrmaFAwR4OCORoUzNGgYI4GBXM0KJijQcEcDQrmaFAwR4OCORoUzNGgYI4+D+a4Z8ZIvbiMEfDbPk6tyab3+WY1zdaGV5UjeMZ+wtN+ciwZt7hrlpayJ9cFvCDgBQEvCHhBwAsCXhDwgoAXBLwgXPOCoLoXf/COd4RAxR+dn/MvEHmYbdPX79LcqGDaDx4lSE+kvqhSqHnCtGcBl8QCrpdawJX4Vz2qcRRw0R41bmMxkW+NmxxFjRs91rgV+Wy9gxc/Xs/TZdPbH/ExxJGcGaeJN+vAWzzPWzfx5h1480/I3Typd1l+t8+KaZ7OFtOHmVuvhZFhV23kVY+q3XVdbRZGpEmjpUXXiNKks9hYTYjVhFhNiNWEWE2I1YRYTYjVhFhNGKiakEp/MKcRzCGYQzCHYA7BHII5BHMI5hDMDQzmPJKFtGNk7oUkCx82efYvo97Q6UKq/adM45QNMmWJf0r+elN2lhK/fNYarN03r1WmbprMySb+5kzQnGfmjD3rDzTWH7zQ+gNG/esPknEk1xnzrz8Yi4m4Z/2BHkX9ARPen7Gj4oEDqXYv/Ex3ECZ96jDUxJigiVvXT9RjHU0a/DQb7mhqxMCf82iq5OxzNGmfyhq7Wj6a3Zg2MU98SmuamF+ttoZPOq53cY31fs1N1i2qZ5YLj7tusvLJJjvW/FTQl9lYyPwUD5mfEiHzUzJkfkqFzE/pkPmpJGx+ahI2QRU4QxX2fbaYhc1R8bBJKhE2SyXDpqlU2DyVDpuoSsK+1jYJ+15b2FwVDfxmGwv7ahsP+26bePauyKl38dHgd2YsPsLiIyw+wuIjLD7C4iMsPsLio9EXH3HmD+YmCOYQzCGYQzCHYA7BHII5BHMI5gYGc9y7LPniyByWJX/WsmQu/KdsglM2yJRJ79LnK3rZF1P6zP0/K++KHvDlmNP/y1qHPgOuVRPLPb+t9eLlhsX2X1qxvfD/JLuxeI3w/CS7sF7zf1NJLo5Z8V26NKpu2opAVWkfeqF9TufWDRGRkpiuZu/r5W4vHl29vFGlHrFhhrFhjA1jbBhjwxgbxtgwxoYxNoyx4WFjw4L7gzmKYA7BHII5BHMI5hDMIZhDMIdgbmAw1yNrTDFrPETWWEj/KWM4ZYNMWY/MNMPM9Jk5tb85KZrzzJz+30829IZyrZSlnHgm+ikm+l9ool/G/on+sXgN9Uz001Ek+mWPrLjAQCoGUjGQioFUDKRiIBUDqRhIxUDqsIFU2SMrzhHMIZhDMIdgDsEcgjkEcwjmEMwNDOZ6ZMUFpliHSLHKHllxjlM2yJT1yIoLTOOembNHVpyjOc/M2SMrLsaR31O+WXGOWfEXmhVXPbLiY/Ea36w4H0VWXPXIiisMpGIgFQOpGEjFQCoGUjGQioFUDKQOG0hVPbLiEsEcgjkEcwjmEMwhmEMwh2AOwdzAYK5HVlxhinWIFKvqkRWXOGWDTFmPrLjCNO6ZOXtkxSWa88ycvp94LjHl+0JTvnriXyihxpHy1T2y4mMxkW9WXI4iK66Zv5MlI1lB3PNo0ng0vdSjSXhuKnocm4r0P5bGsqko731Xj+TrXLT223c1fgnSi913E++NZSxek0z8jiY9ji9BSmLPTQU/cO2lbiqJ5w1Rj+PTxJLjDXG3n5uuVtdzs0wqs8jDaV5omb5N14tZ/hg18eaX8WasjbdR/VszEaD4G0oEYUTcEksljmRAcktyEhNFWElpEluKGoqWVCwItyQjSflvbij4tzCPSNsGVDwpSUbi2JLmf4S7VmVIyi2poW9SkhRIaknzmC5bOZDQmkDf2MpnuhGaWFmS4xAwKKGTimaElu0xsI5t9xjUELSiDXNlmVuauoGMlhRktX1AbtPH8lHQx4kI4gF/5mhKWNlfn4wLEjNa0RRo6mhGWN2HAw3tIDoxUxo72vRxRqIgP3XyU7AudfJQkI06O5kmWslvaS4qmoFsto+VzVmbJk5m6AO/CHd2ALFgXOZo284dXcsDKhGuK5oCTR3NCE+qdg60bTcqEeFkMLRZcU53BnNhflj+YHNWygALhJV8lFs3zNGsWkN8cpwj+AVzalcpyC+czbmV08nMQQZjE0vzo30sLWra8HeLmMPS5c7Opqm2j6WFruhaRzAHEaVTwHoQdTsjclK1c6BtO6wN4dYPT442ATMRWdPmWaeLgLkQbg0Ia8/S2cBVhdML1IB26mgGctp2kFmW7RLanV5CHXWxtKxpTpSTU5zIDOoR6XQE9YAu2xn0L9vrZ6XVhVod5YkuoB5RcUWbZ8t2WEvS+aYEHaXTS4KO0ukrxVEXS6uaNvydXhJ0lE53eaKXpVVNc6K5o0FH5XQB9Yh2uoB6QJftDPqU7XV/UBvkZ46udQH1iI4rmhFdtoOOyumoQEfldFR283U6qhO9FOilnF4K9FJOL3WiiwJdEreHKNBFl+1Wl1K25CgDqEc0q2gKNHU0A5uU7bV9tNXFyaatLk5mDbpopwuwI9rJCeyApo5mIE/ZXsum7REjrGyan/AE3bU7ZmBIosvTAXRP3Lxo2AeSuKJr3WEY6MMcfewPuidO9wT0Tdy+ASygnTn62Af0SpxeSX0+mpM0K9KVOV7ny326zbM1fIvncjZPDZSI4vexePXVq1i8jyevVrNitV+++o75Ya5Lj3fL9Lum67s039mzW0ia8CQRignGFT0c/gdCNVbT
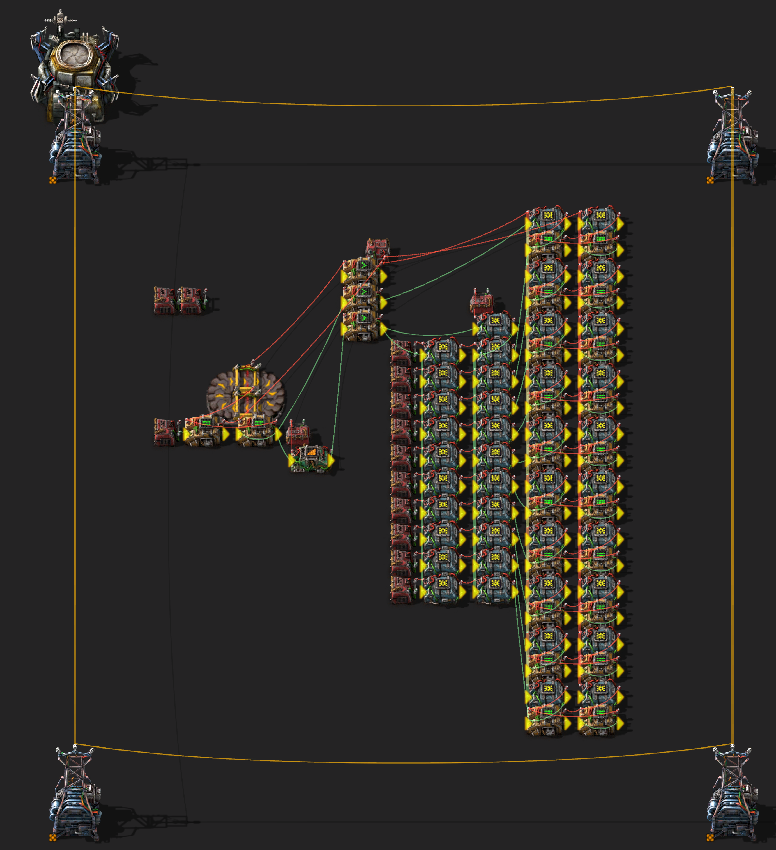
Removing Bias
test bias vs no bias
like same results, so might as well not use bias
simplifies the inference operation, 3 less additions that need to be done in factorio
Factorio Blueprint Generation
explain generating the factorio blueprint directly with weights/biases prepopulated